A spring has a spring constant \(k\). It is cut into two parts \(A\) and \(B\) whose lengths are in the ratio of \(m:1\). The spring constant of the part \(A\) will be:
1. \(\dfrac{k}{m}\)
2. \(\dfrac{k}{m+1}\)
3. \(k\)
4. \(\dfrac{k(m+1)}{m}\)
1. \(\dfrac{k}{m}\)
2. \(\dfrac{k}{m+1}\)
3. \(k\)
4. \(\dfrac{k(m+1)}{m}\)
In damped oscillation, mass is 2 kg and spring constant is 500 N/m and damping coefficient is 1 kg s–1. If the mass is displaced by 20 cm from its mean position and released, then what will be the value of its mechanical energy after 4 seconds?
1. 2.37 J
2. 1.37 J
3. 10 J
4. 5 J
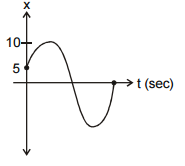
1. \(x= 10\sin\left(\pi t+\frac{\pi}{6}\right)\)
2. \(x= 10\sin\left(\pi t\right)\)
3. \(x= 10\cos\left(\pi t\right)\)
4. \(x= 5\sin\left(\pi t+\frac{\pi}{6}\right)\)
All the surfaces are smooth and the system, given below, is oscillating with an amplitude \({A}.\) What is the extension of spring having spring constant \({k_1},\) when the block is at the extreme position?

| 1. | \(\dfrac{k_1}{ k_1+k_2} A\) | 2. | \(\dfrac{k_2A}{k_1+k_2}\) |
| 3. | \(A\) | 4. | \(\dfrac{A}{2}\) |
| 1. | \(2v_0 \over \sqrt{3}\) | 2. | \(\sqrt{2}v_0 \over 3\) |
| 3. | \({2 \over 3}v_0\) | 4. | \(\sqrt{\frac{2}{3}}v_0\) |
In a simple harmonic oscillation, the graph of acceleration against displacement for one complete oscillation will be:
1. an ellipse
2. a circle
3. a parabola
4. a straight line
\(B\), it returns to \(B\) after another \(3~\text{s}\). The time period of the SHM will be:
| 1. | \(15~\text{s}\) | 2. | \(6~\text{s}\) |
| 3. | \(12~\text{s}\) | 4. | \(9~\text{s}\) |
Acceleration of the particle at \(t = \frac{8}{3}~\text{s}\) from the given displacement \((y)\) versus time \((t)\) graph will be?
1. \(\frac{\sqrt{3}\pi^2}{4}~\text{cm/s}^2\)
2. \(-\frac{\sqrt{3}\pi^2}{4}~\text{cm/s}^2\)
3. \(-\pi^2~\text{cm/s}^2\)
4. zero
| 1. | the gravity of the earth | 2. | the mass of the block |
| 3. | spring constant | 4. | both (2) & (3) |
A body executes oscillations under the effect of a small damping force. If the amplitude of the body reduces by 50% in 6 minutes, then amplitude after the next 12 minutes will be [initial amplitude is ] -
1.
2.
3.
4.





