Q. No.
| 1. | The acceleration is constant and non-zero. |
| 2. | The velocity changes suddenly during the motion. |
| 3. | The velocity is positive throughout. |
| 4. | All of the above are true. |
1. \(1: \sqrt{3}\)
2. \(\sqrt{3}: 1\)
3. \(1:1\)
4. \(1:2\)
| (a) | The particle was released from rest at \(t = 0\). |
| (b) | At \(B,\) the acceleration \(a > 0\). |
| (c) | At \(C,\) the velocity and the acceleration vanish. |
| (d) | Average velocity for the motion between \(A\) and \(D\) is positive. |
| (e) | The speed at \(D\) exceeds that at \(E\). |
Choose the correct option:
| 1. | (b), (c), (d) | 2. | (a), (b), (c), (d) |
| 3. | (a), (d) | 4. | (a), (c), (e) |
Among the four graphs shown in the figure, there is only one graph for which average velocity over the time interval \((0,T)\) can vanish for a suitably chosen \(T\). Select the graph.
| 1. |  |
2. |  |
| 3. |  |
4. |  |
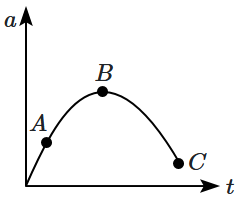
The acceleration (\(a\)) versus time (\(t\)) graph of a particle starting from rest is shown in the figure.
At which point, the velocity of the particle is maximum?
| 1. | \(A\) | 2. | \(B\) |
| 3. | \(C\) | 4. | All of these |
The acceleration \((a)\)-time \((t)\) graph that best suits this motion is:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
| 1. |  |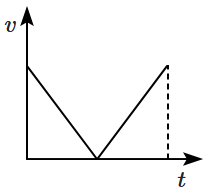
2. |  |
| 3. |  |
4. |  |
Which of the following position-time \((x\text-t)\) graphs may be possible corresponding to given velocity-time \((v\text-t)\) graph?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
The variation of quantity \(A\) with quantity \(B\) is plotted in the given figure which describes the motion of a particle in a straight line.
Consider the following statements:
| (a) | Quantity \(B\) may represent time. |
| (b) | Quantity \(A\) is velocity if motion is uniform. |
| (c) | Quantity \(A\) is displacement if motion is uniform. |
| (d) | Quantity \(A\) is velocity if motion is uniformly accelerated. |
Select the correct option:
1. (a), (b), (c)
2. (b), (c), (d)
3. (a), (c), (d)
4. (a), (c)
© 2025 GoodEd Technologies Pvt. Ltd.