Q. No.| Statement I: | (Newton's 1st Law of Motion) Everybody continues in its state of rest or of uniform motion in a straight line except in so far as it be compelled by an externally impressed force to act otherwise. |
| Statement II: | It is observed that when a car brakes suddenly, the passengers are thrown forward. |
| 1. | Statement I is True, Statement II is True, and Statement I is the correct explanation of Statement II. |
| 2. | Statement I is True, Statement II is True, and Statement I is not the correct explanation of Statement II. |
| 3. | Statement I is True, Statement II is False. |
| 4. | Statement I is False, Statement II is True. |
| Assertion (A): | A standing bus suddenly accelerates. If there was no friction between the feet of a passenger and the floor of the bus, the passenger would move back. |
| Reason (R): | In the absence of friction, the floor of the bus would slip forward under the feet of the passenger. |
| 1. | (A) is True but (R) is False. |
| 2. | (A) is False but (R) is True. |
| 3. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 4. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
A ball is traveling with uniform translatory motion. This means that:
| 1. | it is at rest. |
| 2. | the path can be a straight line or circular and the ball travels with uniform speed. |
| 3. | all parts of the ball have the same velocity (magnitude and direction) and the velocity is constant. |
| 4. | the center of the ball moves with constant velocity and the ball spins about its center uniformly. |
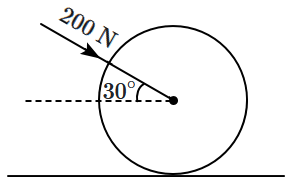
| 1. | \(200~\text{N}\) | 2. | \(600~\text{N}\) |
| 3. | \(800~\text{N}\) | 4. | \(\dfrac{200}{\sqrt{3}}~\text{N}\) |
1. front tyre
2. road
3. rear tyre
4. brakes
An astronaut accidentally gets separated out of his small spaceship, accelerating in interstellar space at a constant rate of \(100~\text{m/s}^2\). What is the acceleration of the astronaut the instant after he is outside the spaceship? (Assume that there are no nearby stars to exert gravitational force on him.)
1. \(0~\text{m/s}^2\)
2.\(100~\text{m/s}^2\)
3.\(10~\text{m/s}^2\)
4.\(1000~\text{m/s}^2\)
| 1. | along south-west | 2. | along eastward |
| 3. | along northward | 4. | along north-east |
A trolley of mass \(300\) kg carrying a sandbag of \(25\) kg is moving uniformly with a speed of \(27\) km/h on a frictionless track. After a while, the sand starts leaking out of a hole on the floor of the trolley at the rate of \(0.05\) kgs–1. What is the speed of the trolley after the entire sandbag is empty?
| 1. | \(27\) km/h | 2. | \(7.7\) km/h |
| 3. | \(20\) km/h | 4. | \(19.6\) km/h |
A hockey player is moving northward and suddenly turns westward at the same speed to avoid an opponent. The force that acts on the player is:
| 1. | frictional force along westward |
| 2. | muscle force along southward |
| 3. | frictional force along south-West |
| 4. | muscle force a south-West |
A boy pushes a box of mass \(2\) kg with a force \(\vec{F} = (20 \hat{i} + 10 \hat{j} )\text{N}\) on a frictionless surface. If the box was initially at rest, then displacement along the \(x\text-\)axis after \(10\) s is:
| 1. | \(250\) m | 2. | \(400\) m |
| 3. | \(500\) m | 4. | \(750\) m |
© 2024 GoodEd Technologies Pvt. Ltd.