Q. No.1. \(39.5\) kJ
2. \(33.5\) kJ
3. \(27.5\) kJ
4. \(6\) kJ
| 1. | adiabatic | 2. | isothermal |
| 3. | isochoric | 4. | isomeric |
| 1. | \(\Delta Q=\Delta U+\Delta W\) |
| 2. | \(\Delta U=\Delta Q+\Delta W\) |
| 3. | \(\Delta U=\Delta Q-\Delta W\) |
| 4. | \(\Delta U+\Delta Q+\Delta W=0\) |
\(1\) mole of rigid diatomic gas performs a work of \(\dfrac{Q}{5}\) when heat \(Q\) is supplied to it. Change in internal energy of the gas is:
| 1. | \(\dfrac{4Q}{5}\) | 2. | \(\dfrac{3Q}{5}\) |
| 3. | \(\dfrac{Q}{5}\) | 4. | \(\dfrac{2Q}{5}\) |
The internal energy change in a system that has absorbed \(2\) kcal of heat and done \(500\) J of work is:
1. \(8900\) J
2. \(6400\) J
3. \(5400\) J
4. \(7900\) J
| 1. | work done by the system is \(120\) J. |
| 2. | work done on the system is \(120\) J. |
| 3. | work done by the system is \(80\) J. |
| 4. | work done on the system is \(80\) J. |
The internal energy of a gas is given by \(U=2pV.\) The gas expands from \(100\) cc to \(200\) cc against a constant pressure of \(10^{5}\) Pa. The heat absorbed by the gas is:
1. \(10\) J
2. \(20\) J
3. \(30\) J
4. \(40\) J
1. \(6000\) J
2. \(9000\) J
3. \(3000\) J
4. zero
Figure shows two processes \(A\) and \(B\) on a system. Let \(\Delta Q_1\) and \(\Delta Q_2\) be the heat given to the system in processes \(A\) and \(B\) respectively. Then:
1. \(\Delta Q_1>\Delta Q_2\)
2. \(\Delta Q_1=\Delta Q_2\)
3. \(\Delta Q_1<\Delta Q_2\)
4. \(\Delta Q_1\leq \Delta Q_2\)
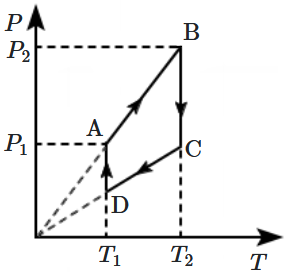
An ideal gas undergoes a cyclic process as shown in the graph between pressure \((P)\) and temperature \((T).\) The part of the graph which represents the absorption of heat from the surrounding are:
| 1. | \(\text{AB, CD}\) | 2. | \(\text{DA, BC}\) |
| 3. | \(\text{DA, AB}\) | 4. | \(\text{BC, AB}\) |
© 2024 GoodEd Technologies Pvt. Ltd.