- 1(current)
Q. No.The restoring force of a spring, with a block attached to the free end of the spring, is represented by:
| 1. |  |
2. |  |
| 3. |  |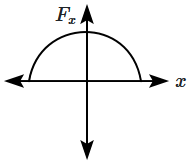
4. |  |
Subtopic: Â Spring mass system |
 66%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A block of mass \(m\) is pushed towards a spring of spring constant \(k,\) with a speed \(u.\) It is very close to the spring, initially. After a time \(t,\) the block rebounds and returns to its initial position. If \(u\) is increased, then:
| 1. | \(t\) increases. |
| 2. | \(t\) decreases. |
| 3. | \(t\) remains unchanged. |
| 4. | the effect on \(t\) cannot be determined due to insufficient information. |
Subtopic: Â Spring mass system |
 59%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
The time period of oscillation of a given spring mass-string system is:
1. \(\pi \sqrt{\dfrac{m}{3 k}}+\pi \sqrt{\dfrac{m}{2 k}}\)
2. \(2 \pi \sqrt{\dfrac{m}{3 k}}\)
3. \(2 \pi \sqrt{\dfrac{m}{3 k}}+2 \pi \sqrt{\dfrac{m}{2 k}}\)
4. \(2 \pi \sqrt{\dfrac{m}{k}}\)
1. \(\pi \sqrt{\dfrac{m}{3 k}}+\pi \sqrt{\dfrac{m}{2 k}}\)
2. \(2 \pi \sqrt{\dfrac{m}{3 k}}\)
3. \(2 \pi \sqrt{\dfrac{m}{3 k}}+2 \pi \sqrt{\dfrac{m}{2 k}}\)
4. \(2 \pi \sqrt{\dfrac{m}{k}}\)
Subtopic: Â Spring mass system |
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A block is connected to a spring and the system is suspended from the ceiling. The extension in the spring in equilibrium is \(x\). If the system is allowed to oscillate vertically, then its time period is:
1. \(\sqrt{\dfrac{2x}{g}}\)
2. \(\sqrt{\dfrac{x}{2g}}\)
3. \(\sqrt{\dfrac{\pi^2x}{g}}\)
4. \(\sqrt{\dfrac{4\pi^2x}{g}}\)
Subtopic: Â Spring mass system |
 78%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A block of mass \(0.2~\text{kg}\) slides without friction on a \(30^{\circ}\) incline and is connected at the top by a massless spring of spring constant \(80~\text{N/m}\) as shown. If the block is pulled slightly down the incline and released, the time period of the ensuing motion is:
1. \( \dfrac{\pi}{2} ~\text{s}\)
2. \( \dfrac{\pi}{5} ~\text{s}\)
3. \( \dfrac{\pi}{10}~\text{s}\)
4. \( \dfrac{\pi}{4}~\text{s}\)
1. \( \dfrac{\pi}{2} ~\text{s}\)
2. \( \dfrac{\pi}{5} ~\text{s}\)
3. \( \dfrac{\pi}{10}~\text{s}\)
4. \( \dfrac{\pi}{4}~\text{s}\)
Subtopic: Â Spring mass system |
 89%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A spring having a spring constant of \(1200\) N/m is mounted on a horizontal table as shown in the figure. A mass of \(3\) kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of \(2.0\) cm and released. The frequency of oscillations will be:
| 1. | \(3.0~\text{s}^{-1}\) | 2. | \(2.7~\text{s}^{-1}\) |
| 3. | \(1.2~\text{s}^{-1}\) | 4. | \(3.2~\text{s}^{-1}\) |
Subtopic: Â Spring mass system |
 73%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A vertical mass-spring system executes simple harmonic oscillations with a period of \(2\) s. A quantity of this system which exhibits simple harmonic variation with a period of \(1\) s is:
| 1. | velocity |
| 2. | potential energy |
| 3. | phase difference between acceleration and displacement |
| 4. | difference between kinetic energy and potential energy |
Subtopic: Â Spring mass system |
 60%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
- 1(current)
Q. No.
© 2024 GoodEd Technologies Pvt. Ltd.