- 1(current)
Q. No.The time period of the given spring-mass system is:
| 1. | \(2\pi \sqrt{\dfrac{m}{k}}\) | 2. | \(2\pi \sqrt{\dfrac{m}{2k}}\) |
| 3. | \(2\pi \sqrt{\dfrac{2m}{\sqrt{3}k}}\) | 4. | \(\pi \sqrt{\dfrac{m}{k}}\) |
1. \(20k\)
2. \(40k\)
3. \(k/2\)
4. none of these
1. \(3\)
2. \(4\)
3. \(2\)
4. \(1\)
Two identical springs of spring constant \(k\) are attached to a block of mass \(m\) and to fixed supports as shown in the figure. When the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. The period of oscillations is:
1. \(2 \pi \sqrt{\dfrac{{m}}{4{k}}}\)
2. \(2 \pi \sqrt{\dfrac{2{m}}{{k}}}\)
3. \(2 \pi \sqrt{\dfrac{{m}}{2{k}}}\)
4. \(2 \pi \sqrt{\dfrac{{m}}{{k}}}\)
When a mass \(m\) is connected individually to two springs \(S_1\) and \(S_2,\) the oscillation frequencies are \(\nu_1\) and \(\nu_2.\) If the same mass is attached to the two springs as shown in the figure, the oscillation frequency would be:
| 1. | \(v_2+v_2\) | 2. | \(\sqrt{v_1^2+v_2^2}\) |
| 3. | \(\left(\dfrac{1}{v_1}+\dfrac{1}{v_1}\right)^{-1}\) | 4. | \(\sqrt{v_1^2-v_2^2}\) |
1. \(0.314~\text s\)
2. \(3.14~\text s\)
3. \(0.628~\text s\)
4. \(0.157~\text s\)
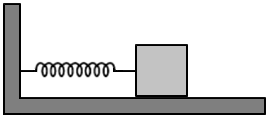
A spring having a spring constant of \(1200\) N/m is mounted on a horizontal table as shown in the figure. A mass of \(3\) kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of \(2.0\) cm and released. The maximum acceleration of the mass is:
| 1. | \(6\) ms–2 | 2. | \(8\) ms–2 |
| 3. | \(3.3\) ms–2 | 4. | \(5.1\) ms–2 |
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.