Q. No.Given the equation of a travelling wave in a string is \(y=0.04\sin(4x-2t),\) where \(y\) and \(x\) are in metre and \(t\) is in seconds. The equation for the velocity of oscillation of particle of string at \(x = x_{0},\) is:
1. \(0.16 \cos(4x_0-2t)\)
2. \(-0.16 \sin(4x_0-2t)\)
3. \(0.04 \cos(4x_0-2t)\)
4. \(-0.08\cos(4x_0-2t)\)
1. \(0.16 \cos(4x_0-2t)\)
2. \(-0.16 \sin(4x_0-2t)\)
3. \(0.04 \cos(4x_0-2t)\)
4. \(-0.08\cos(4x_0-2t)\)
Subtopic: Travelling Wave on String |
63%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A wave travelling along a string is described by, \(y(x,t)=0.005 \text{ sin}(80.0x-3.0t),\) in which the numerical constants are in SI units. The wavelength and the period of the wave respectively are:
1. \(7.85 ~\text{cm}\) and \(2.09 ~\text{s}\)
2. \(7.85 ~\text{cm}\) and \(1.09 ~\text{s}\)
3. \(7.85 ~\text{cm}\) and \(0.09 ~\text{s}\)
4. none of these
Subtopic: Travelling Wave on String |
77%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
Links
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A wave travelling along a string is described by, \(y(x,~t)=0.005 ~\sin(80.0x-3.0t),\) in which the numerical constants are in SI units. The displacement \(y\) of the wave at a distance \(x = 30.0~\text {cm}\) and time \(t=20~\text{s}\) is:
1. \(0.5~\text{mm}\)
2. \(5~\text{mm}\)
3. \(5~\text{m}\)
4. \(5~\text{cm}\)
Subtopic: Travelling Wave on String |
68%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
Links
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
If the initial tension on a stretched string is doubled, then the ratio of the initial and final speeds of a transverse wave along the string is:
1. \(1:2\)
2. \(1:1\)
3. \(\sqrt{2}:1\)
4. \(1:\sqrt{2}\)
1. \(1:2\)
2. \(1:1\)
3. \(\sqrt{2}:1\)
4. \(1:\sqrt{2}\)
Subtopic: Travelling Wave on String |
72%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A heavy uniform rope is suspended from the ceiling, and a block equal to \(3\) times the mass of the rope is suspended from the bottom. The ratio of the speed of a transverse pulse at the top \((v_t)\) to its speed at the bottom \((v_b)\) of the rope, \(\dfrac{v_t}{v_b}=\)
1. \(\dfrac43\)
2. \(\sqrt{\dfrac43}\)
3. \(\dfrac34\)
4. \(\sqrt{\dfrac34}\)
1. \(\dfrac43\)
2. \(\sqrt{\dfrac43}\)
3. \(\dfrac34\)
4. \(\sqrt{\dfrac34}\)
Subtopic: Travelling Wave on String |
77%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A metallic wire with mass per unit length \(6\times 10^{-3}~\text{kg/m}\) is under the tension of \(60~\text N.\) What is the speed of transverse wave in the wire?
| 1. | \(100~\text{m/s}\) | 2. | \(500~\text{m/s}\) |
| 3. | \(600~\text{m/s}\) | 4. | \(10,000~\text{m/s}\) |
Subtopic: Travelling Wave on String |
90%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A string with a mass \(2.50~\text{kg}\) is under a tension of \(200~\text{N}.\) The length of the stretched string is \(20.0~\text{m}\). If the transverse jerk is struck at one end of the string, how long does it take for the disturbance to reach the other end?
| 1. | \(0.5~\text{s}\) | 2. | \(0.6~\text{s}\) |
| 3. | \(0.4~\text{s}\) | 4. | \(0.1~\text{s}\) |
Subtopic: Travelling Wave on String |
69%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
Links
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A heavy uniform rope \(PQ\) is suspended from the ceiling. The lowest end of the rope is given a sharp transverse "shake" (or vibration) so as to cause a pulse. This pulse travels upward. As it travels upward, its speed:
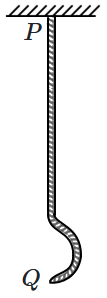
| 1. | increases | 2. | decreases |
| 3. | first increases and then decreases | 4. | remains constant |
Subtopic: Travelling Wave on String |
57%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A string of length \(1~\text m\) and mass per unit length \(0.001~\text{Kg/m}\) is hanging vertically as shown. A small pulse is generated at its lower end. The pulse reaches the top end in approximately:
(take \(g=10~\text{m/s}^2\) )
1. \({\dfrac {1} {\sqrt {10}}}~\text s\)
2. \({\dfrac{3} {\sqrt {10}}} ~\text s\)
3. \( {\sqrt{\dfrac{2}{5}}} ~\text s\)
4. \(\dfrac {\sqrt {5}} 2~\text s\)
(take \(g=10~\text{m/s}^2\) )
1. \({\dfrac {1} {\sqrt {10}}}~\text s\)
2. \({\dfrac{3} {\sqrt {10}}} ~\text s\)
3. \( {\sqrt{\dfrac{2}{5}}} ~\text s\)
4. \(\dfrac {\sqrt {5}} 2~\text s\)
Subtopic: Travelling Wave on String |
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A steel wire \(0.72~\text{m}\) long has a mass of \(5\times10^{-3}~\text{kg}\). If the wire is under tension of \(60~\text{N}\), the speed of transverse waves on the wire will be:
1. \(85~\text{m/s}\)
2. \(83~\text{m/s}\)
3. \(93~\text{m/s}\)
4. \(100~\text{m/s}\)
Subtopic: Travelling Wave on String |
74%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
Links
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
© 2025 GoodEd Technologies Pvt. Ltd.