The acceleration of an electron due to the mutual attraction between the electron and a proton when they are \(1.6~\mathring{A}\) apart is:
\(\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9~ \text{Nm}^2 \text{C}^{-2}\right)\)
| 1. | \( 10^{24} ~\text{m/s}^2\) | 2 | \( 10^{23} ~\text{m/s}^2\) |
| 3. | \( 10^{22}~\text{m/s}^2\) | 4. | \( 10^{25} ~\text{m/s}^2\) |

The magnitude of the electrostatic force of attraction between them is:
| 1. | \(\dfrac{1}{3}kq^{2}\) | 2. | \(\dfrac34kq^2\) |
| 3. | \(\dfrac49kq^2\) | 4. | \(\dfrac29kq^2\) |
| 1. | increased by a factor of \(2\) |
| 2. | decreased by a factor of \(2\) |
| 3. | unchanged |
| 4. | increased by a factor of \(4\) |
In the figure given below, two positive charges \(q_2\) and \(q_3\) fixed along the \(y\)-axis, exert a net electric force in the \(+x\text-\)direction on a charge \(q_1\) fixed along the \(x\)-axis. If a positive charge \(Q\) is added at \((x, 0),\) the force on \(q_1\):

| 1. | shall increase along the positive \(x\)-axis. |
| 2. | shall decrease along the positive \(x\)-axis. |
| 3. | shall point along the negative \(x\)-axis. |
| 4. | shall increase but the direction changes because of the intersection of \(Q\) with \(q_2\) and \(q_3\). |
A charged metallic sphere \(A\) is suspended by a nylon thread. Another identical charged metallic sphere \(B\) held by an insulating handle is brought close to \(A\) such that the distance between their centres is \(10\) cm, as shown in Fig.(a). The resulting repulsion of \(A\) is noted. Then spheres \(A\) and \(B\) are touched by identical uncharged spheres \(C\) and \(D\) respectively, as shown in Fig.(b). \(C\) and \(D\) are then removed and \(B\) is brought closer to \(A\) to a distance of \(5.0\) cm between their centres, as shown in Fig. (c). What is the expected repulsion on \(A\) on the basis of Coulomb’s law?
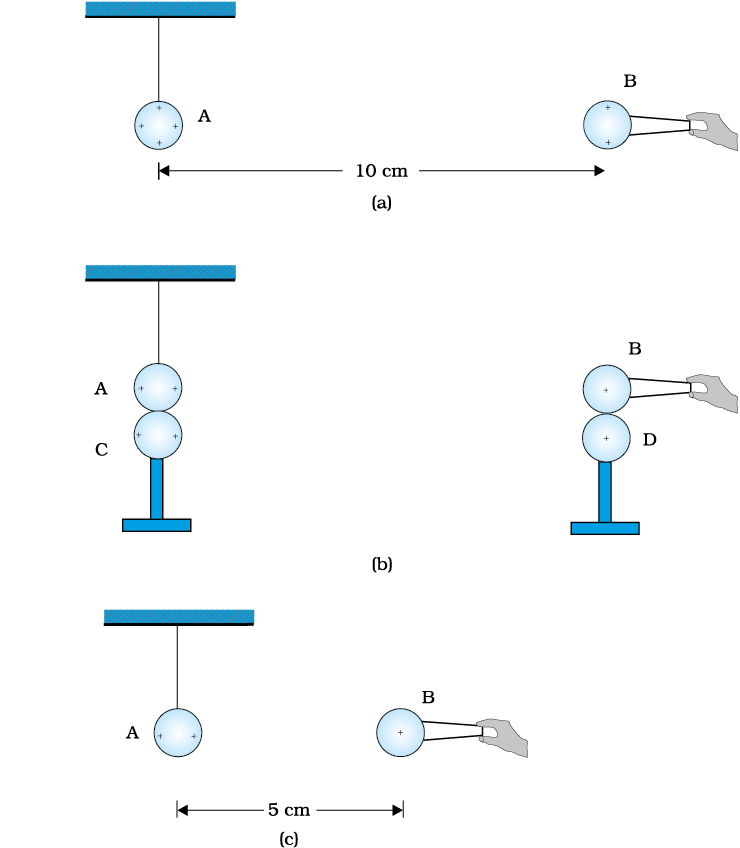
| 1. | Electrostatic force on \(A\) due to \(B\) remains unaltered. |
| 2. | Electrostatic force on \(A\) due to \(B\) becomes double. |
| 3. | Electrostatic force on \(A\) due to \(B\) becomes half. |
| 4. | Can't say. |
1. \(2\) N
2. \(1\) N
3. \(5\) N
4. \(0\) N
| 1. | \(\frac{4F}{3}\) | 2. | \(F\) |
| 3. | \(\frac{9F}{16}\) | 4. | \(\frac{16F}{9}\) |
(Given that the charge of the proton and electron each \(=1.6\times 10^{-19},\) the mass of the electron \(=9.11\times 10^{-31}~\text{kg},\) the mass of the proton \(=1.67\times 10^{-27}~\text{kg}\) )
| 1. | \(10^{20}\) | 2. | \(10^{30}\) |
| 3. | \(10^{40}\) | 4. | \(10\) |
The ratio of the magnitude of electric force to the magnitude of gravitational force for an electron and a proton will be:
(\(m_p=1.67\times10^{-27}~\text{kg}\), \(m_e=9.11\times10^{-31}~\text{kg}\))
1. \(2.4\times10^{39}\)
2. \(2.6\times10^{36}\)
3. \(1.4\times10^{36}\)
4. \(1.6\times10^{39}\)
1. \(6 \times 10^{-3}~\text{N}\)
2. \(5 \times 10^{-3}~\text{N}\)
3. \(4 \times 10^{-4}~\text{N}\)
4. \(5 \times 10^{-4}~\text{N}\)






