Select Chapter Topics:
Q. No.Six charges \(+q,\) \(-q,\) \(+q,\) \(-q,\) \(+q\) and \(-q\) are fixed at the corners of a hexagon of side \(d\) as shown in the figure. The work done in bringing a charge \(q_0\) to the centre of the hexagon from infinity is:
(\(\varepsilon_0\text-\)permittivity of free space)
(\(\varepsilon_0\text-\)permittivity of free space)
| 1. | zero | 2. | \(\dfrac{-q^2}{4\pi\varepsilon_0d}\) |
| 3. | \(\dfrac{-q^2}{4\pi\varepsilon_0d}\Big(3-\dfrac{1}{\sqrt2}\Big)\) | 4. | \(\dfrac{-q^2}{4\pi\varepsilon_0d}\Big(6-\dfrac{1}{\sqrt2}\Big)\) |
Subtopic: Electric Potential Energy |
82%
From NCERT
NEET - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
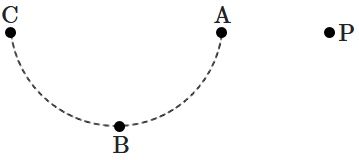
Consider the situation of the figure. The work done in taking a point charge from \(\mathrm{P}\) to \(\mathrm{A}\) is \(W_{\mathrm{A}}\) , from \(\mathrm{P}\) to \(\mathrm{B}\) is \(W_{\mathrm{B}}\) and from \(\mathrm{P}\) to \(\mathrm{C}\) is \(W_{\mathrm{C}}\). Then:
| 1. | \(W_{\mathrm{A}}<W_{\mathrm{B}}<W_{\mathrm{C}}\) | 2. | \(W_{\mathrm{A}}>W_{\mathrm{B}}>W_{\mathrm{C}}\) |
| 3. | \(W_{\mathrm{A}}=W_{\mathrm{B}}=W_{\mathrm{C}}\) | 4. | none of these |
Subtopic: Electric Potential Energy |
64%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
Links
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A particle of mass \(0.002\) kg and charge \(1 ~\mu\text{C}\) is held at rest on a frictionless horizontal surface at a distance of \(1\) m from a fixed charge of \(1\) mC. If the particle is released, it will be repelled. The speed of the particle when it is at a distance of \(10\) m from the fixed charge will be:
| 1. | \(60\) ms–1 | 2. | \(75\) ms–1 |
| 3. | \(90\) ms–1 | 4. | \(100\) ms–1 |
Subtopic: Electric Potential Energy |
81%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
As per the figure a point charge \(+q\) is placed at the origin \(\mathrm{O}\). Work done in taking another point charge \(-Q\) from the point \(\mathrm{A}(0, \mathrm{a})\) to another point \(\mathrm{B}(\mathrm{a},0)\) along the straight path \(\mathrm{AB}\) is:
1. \(\Big(\dfrac{-qQ}{4\pi\varepsilon_0}\dfrac{1}{a}\Big)\sqrt {2}\)
2. \(\Big(\dfrac{qQ}{4\pi\varepsilon_0}\dfrac{1}{a}\Big)\sqrt{2}\)
3. \(\Big(\dfrac{qQ}{4\pi\varepsilon_0}\dfrac{1}{a}\Big)\dfrac{1}{\sqrt{2}}\)
4. zero
1. \(\Big(\dfrac{-qQ}{4\pi\varepsilon_0}\dfrac{1}{a}\Big)\sqrt {2}\)
2. \(\Big(\dfrac{qQ}{4\pi\varepsilon_0}\dfrac{1}{a}\Big)\sqrt{2}\)
3. \(\Big(\dfrac{qQ}{4\pi\varepsilon_0}\dfrac{1}{a}\Big)\dfrac{1}{\sqrt{2}}\)
4. zero
Subtopic: Electric Potential Energy |
79%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
A thin semi-circular ring of radius \(r\) has a positive charge \(q\) distributed uniformly over it. The net potential at the centre \(O\) is:
| 1. | \(-\dfrac{q}{2 \pi^{} \varepsilon_{0} r^{}} \) | 2. | \(-\dfrac{q}{4 \pi^{} \varepsilon_{0} r^{}} \) |
| 3. | \(\dfrac{q}{4 \pi^{} \varepsilon_{0} r^{}} \) | 4. | \(0\) |
Subtopic: Electric Potential |
54%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A neutral spherical copper particle has a radius of \(10\) nm (\(1\) nm = \(10^{-9}\) m). It gets charged by applying the voltage slowly adding one electron at a time. Then the graph of the total charge on the particle vs the applied voltage would look like:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Subtopic: Electric Potential |
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
If a conducting sphere of radius \(R\) is charged. Then the electric field at a distance \(r(r>R)\) from the centre of the sphere would be, (\(V=\) potential on the surface of the sphere):
| 1. | \(\dfrac{rV}{R^2}\) | 2. | \(\dfrac{R^2V}{r^3}\) |
| 3. | \(\dfrac{RV}{r^2}\) | 4. | \(\dfrac{V}{r}\) |
Subtopic: Electric Potential |
From NCERT
NEET - 2023
Please attempt this question first.
Hints
Please attempt this question first.
Four identical point charges (\(q\) each) are placed at the four corners of a square of diagonal \(d.\) The potential at a point which is at a distance \(\dfrac{d}{2}\) above the centre of the square is:
\(\Big(k=\dfrac{1}{4\pi\varepsilon_0}\Big)\)
1. \(\dfrac{8~kq}{d}\)
2. \(\dfrac{4~kq}{d}\)
3. \(\dfrac{4\sqrt2~kq}{d}\)
4. \(\dfrac{\sqrt2~kq}{d}\)
\(\Big(k=\dfrac{1}{4\pi\varepsilon_0}\Big)\)
1. \(\dfrac{8~kq}{d}\)
2. \(\dfrac{4~kq}{d}\)
3. \(\dfrac{4\sqrt2~kq}{d}\)
4. \(\dfrac{\sqrt2~kq}{d}\)
Subtopic: Electric Potential |
69%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
Two charged conducting spheres of radii a and b are connected to each other by a wire. The ratio of electric fields at the surfaces of the two spheres is:
| 1. | \(\dfrac{a}{b}\) | 2. | \(1\) |
| 3. | \(\dfrac{2a}{b}\) | 4. | \(\dfrac{b}{a}\) |
Subtopic: Electric Potential |
67%
From NCERT
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
Links
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Two hollow conducting spheres of radii \(R_1\) and \(R_2\) \(\left ( R_1\gg R_2 \right )\) are concentric and have equal charges. The potential would be:
| 1. | dependent on the material property of the sphere |
| 2. | more on the bigger sphere |
| 3. | more on the smaller sphere |
| 4. | equal on both the spheres |
Subtopic: Electric Potential |
72%
From NCERT
PMT - 2022
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2025 - Target Batch
Select Chapter Topics:
© 2024 GoodEd Technologies Pvt. Ltd.