Which one is not an example of a point object?
| 1. | A railway carriage moving without jerks between two stations. |
| 2. | A monkey sitting on top of a man cycling smoothly on a circular track. |
| 3. | A plane under a journey of several thousand kilometres. |
| 4. | A tumbling beaker that has slipped off the edge of a table. |
A drunkard walking in a narrow lane takes \(5\) steps forward and \(3\) steps backward, followed again by \(5\) steps forward and \(3\) steps backward, and so on. Each step is \(1\) m long and requires \(1\) s. There is a pit on the road \(13\) m away from the starting point. The drunkard will fall into the pit after:
1. \(37\) s
2. \(31\) s
3. \(29\) s
4. \(33\) s
The speed-time graph of a particle moving along a fixed direction is shown in the figure. Then the distance traversed by the particle between \(t=0\) s to \(10\) s is:
1. \(70\) m
2. \(60\) m
3. \(50\) m
4. \(40\) m
The velocity-time graph of a particle in one-dimensional motion is shown in the figure. Which of the following formulae is correct for describing the motion of the particle over the time interval \(t_1\) to \(t_2?\)

| 1. | \(x\left(t_2\right)=x\left(t_1\right)+v\left(t_1\right)\left(t_2-t_1\right)+\left(\frac{1}{2}\right) a\left(t_2-t_1\right)^2\) |
| 2. | \({v}\left({t}_2\right)={v}\left({t}_1\right)+{a}\left({t}_2-{t}_1\right)\) |
| 3. | \(\small{x\left(t_2\right)=x\left(t_1\right)+v_{\text {average }}\left(t_2-t_1\right)+\left(\frac{1}{2}\right) a_{\text {average }}\left(t_2-t_1\right)^2\small}\) |
| 4. | \({v}_{\text {average }}=\left[{x}\left({t}_2\right)-{x}\left({t}_1\right)\right] /\left({t}_2-{t}_1\right)\) |
The figure gives the x-t plot of a particle executing a one-dimensional simple harmonic motion. Then the signs of position & velocity variables of the particle at t = -1.2 sec respectively are:
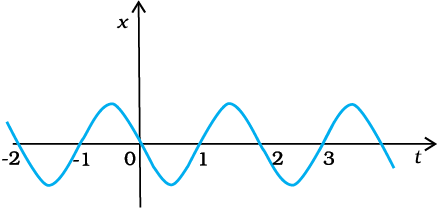
\(\left(1\right) positive , negative\)
\(\left(2\right) positive , positive\)
\(\left(3\right) negative , positive\)
\(\left(4\right) negative , negative\)
The position-time \((x\text-t)\) graphs for two children \(A\) and \(B\) returning from their school \(O\) to their homes \(P\) and \(Q\) respectively are shown in the graph.

Choose the incorrect statement:
| 1. | \(B\) reaches home faster than \(A.\) |
| 2. | \(B\) overtakes \(A\) on the road twice. |
| 3. | \(B\) walks faster than \(A.\) |
| 4. | \(A\) lives closer to the school than \(B.\) |
A jet airplane travelling at the speed of \(500~\text{km/h}\) ejects its products of combustion at the speed of \(1500~\text{km/h}\) relative to the jet plane. What is the speed of the latter with respect to an observer on the ground?
1. \(1000~\text{km/h}\)
2. \(500~\text{km/h}\)
3. \(1500~\text{km/h}\)
4. \(2000~\text{km/h}\)
A car moving along a straight highway at a speed of \(126~\text{km/h}\) is brought to a stop within a distance of \(200~\text{m}.\) How long does it take for the car to stop?
1. \(10.2~\text{s}\)
2. \(9.6~\text{s}\)
3. \(11.4~\text{s}\)
4. \(6.7~\text{s}\)
Two trains \(A\) and \(B\) of length \(400~\text m\) each are moving on two parallel tracks with a uniform speed of \(72~\text{km/h}\) in the same direction with \(A\) ahead of \(B.\) The driver of \(B\) decides to overtake \(A\) and accelerates by \(1~\text{m/s}^2.\) If after \(50~\text s,\) the guard of \(B\) just brushes past the driver of \(A,\) what was the original distance between them?
1. \(2000~\text m\)
2. \(2250~\text m\)
3. \(1200~\text m\)
4. \(1250~\text m\)
On a two-lane road, car \(A\) is travelling at a speed of \(36\) kmh–1. Two cars \(B\) and \(C\) approach car \(A\) in opposite directions with a speed of \(54\) kmh–1 each. At a certain instant, when the distance \(AB\) is equal to \(AC\), both being \(1\) km, \(B\) decides to overtake \(A\) before \(C\) does. What minimum acceleration of car \(B\) is required to avoid an accident?
1. \(1\) ms–2
2. \(5\) ms–2
3. \(2\) ms–2
4. \(3\) ms–2







