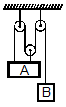
A block A of mass 7 kg is placed on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 3 kg at the other end. The acceleration of the system is (given g = 10 ms^–2) 

1. 100 ms^–2

2. 3 ms^–2

3. 10 ms^–2

4. 30 ms^–2

In the arrangement shown, the ends \(P\) and \(Q\) of an inextensible string move downwards with uniform speed \(v.\) The pulleys \(A\) and \(B\) are fixed. The mass \(M\) moves upward with a speed of:

    
1. \(2 v \cos \theta\)
2. \(v \cos \theta\)
3. \(\left(\frac{2 v}{\cos \theta}\right)\)
4. \(\left(\frac{v}{\cos \theta}\right)\)

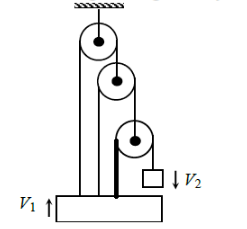
1. \(7v_1-v_2=0\)
2. \(7v_1+v_2=0\)
3. \(v_1+v_2=0\)
4. \(v_1+3v_2=0\)

Using constraint equations relation between $a_1$ and $a_2$ will be 

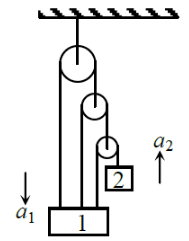
1. $a_1$ =3$a_2$

2. a$a_2$ =3$a_1$

3. a$a_2$= 6$a_1$

4. a$a_2$= 7$a_1$

A string with constant tension T is deflected through an angle $2{\theta }_0$ by a smooth fixed pulley. The force on the pulley is

$\left(\mathrm{a}\right) 2\mathrm{T} {\mathrm{cos\theta }}_0$
$\left(\mathrm{b}\right) \mathrm{T} {\mathrm{cos\theta }}_0$
$\left(\mathrm{c}\right) 2\mathrm{T} {\mathrm{sin\theta }}_0$
$\left(\mathrm{d}\right) \mathrm{T} {\mathrm{sin\theta }}_0$

In the figure pulley ${\mathrm{P}}_1$ is fixed and the pulley ${\mathrm{P}}_2$ is movable. If ${\mathrm{w}}_1={\mathrm{w}}_2$, what is the angle between ${\mathrm{AP}}_2{\mathrm{P}}_1$? (pulleys are frictionless)

         
1. 30°

2. 60°

3. 150°

4. 120°

Two blocks of masses \(2\) kg and \(3\) kg are tied at the ends of a light inextensible string passing over a frictionless pulley as shown.

If the system is accelerating upward with acceleration \(5\) m/s², the tension in the string is:
1. \(24\) N
2. \(36\) N
3. \(48\) N
4. \(18\)N

The pulleys and string shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle \(\theta\) should be:

      

1. 0°
2. 30$°$
3. 45$°$
4. 60$°$

At a given instant, A is moving with velocity of 5 m/s upwards. What is velocity of B at this time?

1. 15 m/s $\downarrow$

2. 15 m/s $\uparrow$

3. 5 m/s $\downarrow$

4. 5 m/s $\uparrow$

The blocks \(A\) and \(B\) are shown in figure have masses \(5\) kg and \(4\) kg respectively. The system is released from rest. The speed of \(B\) after \(A\) has travelled a distance \(1\) m along the incline is: (take \(g = 10~\text{m/s}^2\), pulleys and strings are ideal and plane is smooth)

 
1. \(\sqrt{\frac{6}{5}}~\text{m/s}\)
2. \(\sqrt{\frac{3}{2}}~\text{m/s}\)
3. \(\sqrt{\frac{5}{6}}~\text{m/s}\)
4. \(\sqrt{\frac{2}{3}}~\text{m/s}\)