Please be patient as the PDF generation may take upto a minute.

A particle is projected at an angle $\theta$ with horizontal with an initital speed u. When it makes an angle $\alpha$ with horizontal, its speed v is-
1. $u\cos \theta$
2. $u\cos \theta u\cos \alpha$
3. $\frac{u\sin \theta }{\sin \alpha }$
4. $\frac{u\cos \theta }{\cos \alpha }$
 

A body is projected with velocity $20\sqrt{3}$ m/s with an angle of projection 60$°$ with horizontal. Calculate velocity on that point where body makes an angle 30$°$ with the horizontal.
1. 20 m/s
2. $\frac{20}{\sqrt{3}} m/s$
3. $10\sqrt{3} m/s$
4. 10 m/s

A particle is moving with veocity $\overrightarrow{\mathrm{v}}=\mathrm{k}(\mathrm{y}\hat{\mathrm{i}}+\mathrm{x}\hat{\mathrm{j}})$; where k is constant. The general equation for the path is:
1. $\mathrm{y}={\mathrm{x}}^2+\mathrm{constant}$
2. ${\mathrm{y}}^2={\mathrm{x}}^2+\mathrm{constant}$
3. $\mathrm{y}=\mathrm{x}+\mathrm{constant}$
4. xy=constant
 

A body thrown vertically so as to reach its maximum height in t second. The total time from the time of projection to reach a point at half of its maximum height while returning (in second) is:
1. $\sqrt{2}t$
2. $\left(1+\frac{1}{\sqrt{2}}\right)t$
3. $\frac{3t}{2}$
4. $\frac{t}{\sqrt{2}}$

A particle is projected with a velocity u making an angle $\mathrm{\theta }$ with the horizontal. At any instant, its velocity v is at right angles to its initial velocity u; then v is:
1.  ucos$\mathrm{\theta }$
2.  utan$\mathrm{\theta }$
3.  ucot$\mathrm{\theta }$
4.  usec$\mathrm{\theta }$

A projectile is given an initial velocity of $\hat{i}+2\hat{j}$. The cartesian equation of its path is (g = 10 ${\mathrm{ms}}^{-2}$) 
1. $\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$
2. $\mathrm{y}=\mathrm{x}-5{\mathrm{x}}^2$
3. $4\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$
4. $\mathrm{y}=2\mathrm{x}-25{\mathrm{x}}^2$

A ship A is moving westwards with a speed of 10 km ${\mathrm{h}}^{-1}$ and a ship B, 100 km south of A is moving northwards with a speed of 10 km ${\mathrm{h}}^{-1}$. The time after which the distance between them becomes the shortest, is:
1. 5 hr
2. $5\sqrt{2}$ hr
3. $10\sqrt{2}$ hr
4. 0 hr

Time taken by the projectile to reach from A to B is t. Then the distance AB is equal to :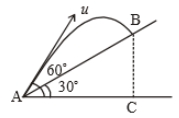

1. $\frac{ut}{\sqrt{3}}$
2. $\frac{\sqrt{3}ut}{2}$
3. $\sqrt{3}ut$
4. 2ut

A particle projected with kinetic energy ${\mathrm{k}}_0$ with an angle of projection $\mathrm{\theta }$. Then the variation of kinetic K with vertical displacement y is
1.  linear
2.  parabolic
3.  hyperbolic
4.  periodic

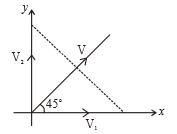
Three particles moving with constant velocities ${\mathrm{V}}_1, {\mathrm{V}}_2$ and V respectively as given in the figure. After some time all three particles are in the same line, then relation among ${\mathrm{V}}_1, {\mathrm{V}}_2$ and V is
                                     
1.  $\mathrm{V} = {\mathrm{V}}_1 + {\mathrm{V}}_2$
2.  $\mathrm{V} = \sqrt{{\mathrm{V}}_1{\mathrm{V}}_2}$
3.  $\mathrm{V} = \frac{{\mathrm{V}}_1{\mathrm{V}}_2}{{\mathrm{V}}_1+{\mathrm{V}}_2}$
4.  $\mathrm{V} = \frac{\sqrt{2}{\mathrm{V}}_1{\mathrm{V}}_2}{{\mathrm{V}}_1+{\mathrm{V}}_2}$

A river is flowing with a speed of 1 km/hr. A swimmer wants to go to point 'C' starting from 'A'. He swims with a speed of 5 km/hr, at an angle $\theta$ with respect to the river. If \(\text {AB = BC = 400 m}\). Then

1. The time taken by the man is 12 min
2. The time taken by the man is 8 min
3. The value of $\theta$ is 45$°$
4. The value of $\theta$ is 53$°$

 A body is thrown horizontally with a velocity \(\sqrt{2 g h}\) from the top of a tower of height \(h\). It strikes the level ground through the foot of the tower at a distance \(x\) from the tower. The value of \(x\) is:

A particle starts from the origin at t=0 and moves in the x-y plane with constant acceleration 'a' in the y direction. Its equation of motion is $y=b{x}^2$. The x component of its velocity (at t=0) is:
(1) variable
(2) $\sqrt{\frac{2a}{b}}$
(3) $\frac{a}{2b}$
(4) $\sqrt{\frac{a}{2b}}$

A body is projected with a velocity \(u\) with an angle of projection \(\theta.\) The change in velocity after the time \((t)\) from the time of projection will be:

A particle has initial velocity $\left(3\hat{\mathrm{i}}+4\hat{\mathrm{j}}\right)$ and has acceleration $\left(0.4\hat{\mathrm{i}}+0.3\hat{\mathrm{j}}\right)$. Its speed after 10 s:
1. 7 units
2. $7\sqrt{2}$ units
3. 8.5 units
4. 10 units

The gravity in space is given by $\overrightarrow{\mathrm{g}}=-10 \hat{j} m{s}^{-2}$. Two particles are simultaneously projected with velocity $\overrightarrow{{\mathrm{u}}_1}=\left(10 m{s}^{-1}\right)\hat{i}+\left(10 m{s}^{-1}\right)\hat{j}$ and $\overrightarrow{{\mathrm{u}}_2}=\left(20 m{s}^{-1}\right)\hat{i}+\left(10 m{s}^{-1}\right)\hat{j}$. Then, the ratio of their times of flight
1. 1:1
2. 1:2
3. 2:1
4. none

The x and y coordinates of a particle at any time t are given by $x=7t+4t^2$ and y = 5t, where x and y are in metre and t in seconds. The acceleration of particle at t = 5s is  
(1) Zero
(2) 8 m/s²
(3) 20 m/s²
(4) 40 m/s²

A boat is sent across a river in perpendicular direction with a velocity of 8 km/hr. If the resultant velocity of boat is 10 km/hr, then velocity of the river is : 
(1) 10 km/hr
(2) 8 km/hr
(3) 6 km/hr
(4) 4 km/hr

A boat moves with a speed of 5 km/h relative to water in a river flowing with a speed of 3 km/h and having a width of 1 km. The minimum time taken around a round trip(returning to the initial point) is:
(1) 5 min
(2) 60 min
(3) 20 min
(4) 30 min

A river is flowing from W to E with a speed of 5 m/min. A man can swim in still water with a velocity 10 m/min. In which direction should the man swim so as to take the shortest possible path to go to the south. 
(1) 30° with downstream
(2) 60° with downstream
(3) 120° with downstream
(4) South

A train is moving towards east and a car is along north, both with same speed. The observed direction of car to the passenger in the train is 
(1) East-north direction
(2) West-north direction
(3) South-east direction
(4) None of these

A stone is just released from the window of a train moving along a horizontal straight track. The stone will hit the ground following
(1) Straight path
(2) Circular path
(3) Parabolic path
(4) Hyperbolic path

An aeroplane is flying at a constant horizontal velocity of 600 km/hr at an elevation of 6 km towards a point directly above the target on the earth's surface. At an appropriate time, the pilot releases a ball so that it strikes the target at the earth. The ball will appear to be falling
(1) On a parabolic path as seen by pilot in the plane
(2) Vertically along a straight path as seen by an observer on the ground near the target
(3) On a parabolic path as seen by an observer on the ground near the target
(4) On a zig-zag path as seen by pilot in the plane

A bomb is dropped from an aeroplane moving horizontally at constant speed. When air resistance is taken into consideration, the bomb 
(1) Falls to earth exactly below the aeroplane
(2) Fall to earth behind the aeroplane
(3) Falls to earth ahead of the aeroplane
(4) Flies with the aeroplane

An aeroplane is flying horizontally with a velocity u = 600 km/h at a height of 1960 m. When it is vertically at a point A on the ground, a bomb is released from it. The bomb strikes the ground at point B. The distance AB is:
1. 1200 m
2. 0.33 km
3. 3.33 km
4. 33 km

An aeroplane moving horizontally with a speed of 720 km/h drops a food pocket while flying at a height of 396.9 m. The time taken by a food pocket to reach the ground and its horizontal range is (Take g = 9.8 m/sec²)
(1) 3 sec and 2000 m
(2) 5 sec and 500 m
(3) 8 sec and 1500 m
(4) 9 sec and 1800 m

A particle (A) is dropped from a height and another particle (B) is thrown in the horizontal direction with a speed of 5 m/sec from the same height. The correct statement is:
(1) Both particles will reach at ground simultaneously
(2) Both particles will reach at ground with same speed
(3) Particle (A) will reach at ground first with respect to particle (B)
(4) Particle (B) will reach at ground first with respect to particle (A)

A bomber plane moves horizontally with a speed of \(500~\text{m/s}\) and a bomb is released from it. The bomb strikes the ground in \(10~\text{s}\). The angle at which it strikes the ground will be: \((g= 10~\text{m/s}^2)\)
1. \(\tan ^{-1}\left(\frac{1}{5}\right )\)
2. \(\tan \left(\frac{1}{5}\right)\)
3. \(\tan ^{-1}(1)\)
4. \(\tan ^{-1}(5)\)

In the motion of a projectile freely under gravity, its
(1) Total energy is conserved
(2) Momentum is conserved
(3) Energy and momentum both are conserved
(4) None is conserved

The range of a projectile for a given initial velocity is maximum when the angle of projection is 45°. The range will be minimum, if the angle of projection is
(1) 90°
(2) 180°
(3) 60°
(4) 75°

A ball is thrown upwards and it returns to the ground describing a parabolic path. Which of the following remains constant?
(1) Kinetic energy of the ball
(2) Speed of the ball
(3) Horizontal component of velocity
(4) Vertical component of velocity

An object is thrown along a direction inclined at an angle of 45° with the horizontal direction. The horizontal range of the particle is equal to 
(1) Vertical height
(2) Twice the vertical height
(3) Thrice the vertical height
(4) Four times the vertical height

The height y and the distance x along the vertical plane of a projectile on a certain planet (with no surrounding atmosphere) are given by $y=(8t-5t^2)$ meter and x = 6t meter, where t is in second. The velocity with which the projectile is projected is 
(1) 8 m/sec
(2) 6 m/sec
(3) 10 m/sec
(4) Not obtainable from the data

Galileo writes that for angles of projection of a projectile at angles $(45+\theta )$ and $(45-\theta )$, the horizontal ranges described by the projectile are in the ratio of (if $\theta \le 45$) 
1. 2 : 1
2. 1 : 2
3. 1 : 1
4. 2 : 3

A ball is projected with kinetic energy E at an angle of 45° to the horizontal. At the highest point during its flight, its kinetic energy will be 
(1) Zero
(2) $\frac{E}{2}$
(3) $\frac{E}{\sqrt{2}}$
(4) E

At the top of the trajectory of a projectile, the magnitude of the acceleration is
(1) Maximum
(2) Minimum
(3) Zero
(4) g

A body is projected at such an angle that the horizontal range is three times the greatest height. The angle of projection is 
(1) ${25}^o{8}^{\text{'}}$
(2) ${33}^o{7}^{\text{'}}$
(3) ${42}^o{8}^{\text{'}}$
(4) ${53}^o{8}^{\text{'}}$

If the range of a gun that fires a shell with muzzle speed v is R, then the angle of elevation of the gun is 
(1) ${\cos }^{-1}\left(\frac{{\displaystyle v^2}}{{\displaystyle Rg}}\right)$
(2) ${\cos }^{-1}\left(\frac{{\displaystyle gR}}{{\displaystyle v^2}}\right)$
(3) $\frac{1}{2}\left(\frac{{\displaystyle v^2}}{{\displaystyle Rg}}\right)$
(4) $\frac{1}{2}{\sin }^{-1}\left(\frac{{\displaystyle gR}}{{\displaystyle v^2}}\right)$

If a body A of mass M is thrown with a velocity v at an angle of 30° to the horizontal and another body B of the same mass is thrown with the same speed at an angle of 60° to the horizontal. The ratio of horizontal range of A to B will be 
(1) 1 : 3
(2) 1 : 1
(3) $1:\sqrt{3}$
(4) $\sqrt{3}:1$

Four bodies \(P\), \(Q\), \(R\) and \(S\) are projected with equal velocities having angles of projection \(15^{\circ},\) \(30^{\circ},\)\(45^{\circ},\) and \(60^{\circ}\) with the horizontal respectively. The body having the shortest range is? 

A stone projected with a velocity \(u\) at an angle \(\theta\) with the horizontal reaches maximum height \(H_1.\) When it is projected with velocity \(u\) at an angle \(\left(\frac{\pi}{2}-\theta\right)\) with the horizontal, it reaches maximum height \(H_2.\) The relation between the horizontal range of the projectile \(R\) and \(H_1\) and \(H_2\) is: 

The equation of motion of a projectile is given by x = 36 t metre and 2y = 96 t – 9.8 t² metre. The angle of projection is:
1. ${\sin }^{-1}\left(\frac{{\displaystyle 4}}{{\displaystyle 5}}\right)$
2. ${\sin }^{-1}\left(\frac{{\displaystyle 3}}{{\displaystyle 5}}\right)$
3. ${\sin }^{-1}\left(\frac{{\displaystyle 4}}{{\displaystyle 3}}\right)$
4. ${\sin }^{-1}\left(\frac{{\displaystyle 3}}{{\displaystyle 4}}\right)$

For a given velocity, a projectile has the same range of R for two angles of projection. If t₁ and t₂ are the times of flight in the two cases then:
(1) $t_1{t}_2\propto R^2$
(2) $t_1{t}_2\propto R$
(3) $t_1{t}_2\propto \frac{1}{R}$
(4) $t_1{t}_2\propto \frac{1}{R^2}$

A body of mass m is thrown upwards at an angle θ with the horizontal with velocity v. While rising up the velocity of the mass after t seconds will be 
(1) $\sqrt{{\left(v\cos \theta \right)}^2+{\left(v\sin \theta \right)}^2}$
(2) $\sqrt{{(v\cos \theta -v\sin \theta )}^2-gt}$
(3) $\sqrt{v^2+g^2{t}^2-\left(2v\sin \theta \right)gt}$
(4) $\sqrt{v^2+g^2{t}^2-\left(2v\cos \theta \right)gt}$ 

A cricketer can throw a ball to a maximum horizontal distance of \(100~\text{m}\). With the same effort, he throws the ball vertically upwards. The maximum height attained by the ball is: 
1. \(100~\text{m}\)
2. \(80~\text{m}\)
3. \(60~\text{m}\)
4. \(50~\text{m}\)

Figure shows four paths for a kicked football. Ignoring the effects of air on the flight, rank the paths according to initial horizontal velocity component, highest first

(1) 1, 2, 3, 4
(2) 2, 3, 4, 1
(3) 3, 4, 1, 2
(4) 4, 3, 2, 1

The path of a projectile in the absence of air drag is shown in the figure by dotted line. If the air resistance is not ignored , then which one of the paths shown in the figure is appropriate for the projectile ?

1. B
2. A
3. D
4. C

The velocity of a projectile at the initial point A is (2i + 3j) m/s. Its velocity (in m/s) at point B is:

1.  -2i+3j
2.  -2i-3j
3.   2i-3j
4.  2i+3j

A projectile is fired at an angle of 45$°$ with the horizontal. The elevation angle $\alpha$ of the projectile at its highest point as seen from the point of projection is:
1. 60$°$                                           2. ${\tan }^{-1}\left(\frac{1}{2}\right)$
3. ${\tan }^{-1}\left(\frac{\sqrt{3}}{2}\right)$                               4. $45°$

The speed of a projectile at its maximum height is half of its initial speed. The angle of projection is:
1. $60°$                                         
2. $15°$
3. $30°$                                         
4. $45°$