When a proton is released from rest in a room, it starts with an initial acceleration towards the east. When it is projected towards the north with a speed , it moves with initial acceleration towards east. The electric and magnetic fields in the room are -
1.
2.
3.
4.
Which of the following graphs correctly represents the variation of magnetic field induction with distance due to a thin wire carrying current?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
| 1. | the speed will change. |
| 2. | the direction will change. |
| 3. | both (1) and (2) |
| 4. | none of the above |
The electric charge in uniform motion produces :
| 1. | An electric field only |
| 2. | A magnetic field only |
| 3. | Both electric and magnetic field |
| 4. | Neither electric nor magnetic field |
An infinitely long straight conductor is bent into the shape as shown in the figure.
It carries a current of \(i\) amperes and the radius of the circular loop is \(r\) metres. What will be the magnetic induction at its centre?

1. \(\frac{\mu_{0}}{4 \pi} \frac{2 i}{r} \left( \pi + 1 \right)\)
2. \(\frac{\mu_{0}}{4 \pi} \frac{2 i}{r} \left(\pi - 1 \right)\)
3. zero
4. Infinite
| 1. | \(3.33\times 10^{-9}\) Tesla |
| 2. | \(1.11\times 10^{-4}\) Tesla |
| 3. | \(3\times 10^{-3}\) Tesla |
| 4. | \(9\times 10^{-2}\) Tesla |
In the figure shown, the magnetic induction at the centre of the arc due to the current in portion AB will be
1. 3.
2. 4. Zero
In the figure shown below there are two semicircles of radius \(r_1\) and \(r_2\) in which a current \(i\) is flowing. The magnetic induction at the centre of \(O\) will be:
| 1. | \(\dfrac{\mu_{0} i}{r} \left(r_{1} + r_{2}\right)\) | 2. | \(\dfrac{\mu_{0} i}{4} \left[\dfrac{r_{1} + r_{2}}{r_{1} r_{2}}\right]\) |
| 3. | \(\dfrac{\mu_{0} i}{4} \left(r_{1} - r_{2}\right)\) | 4. | \(\dfrac{\mu_{0} i}{4} \left[\dfrac{r_{2} - r_{1}}{r_{1} r_{2}}\right]\) |
The direction of magnetic lines of forces close to a straight conductor carrying current will be:
| 1. | along the length of the conductor. |
| 2. | radially outward. |
| 3. | circular in a plane perpendicular to the conductor. |
| 4. | helical. |
The magnetic field at the centre of a coil of n turns, bent in the form of a square of side 2 l, carrying current i, is :
1. 2.
3. 4.
A wire carrying current i is shaped as shown. Section AB is a quarter circle of radius r. The magnetic field is directed :
1. At an angle to the plane of the paper
2. Perpendicular to the plane of the paper and directed in to the paper
3. Along the bisector of the angle ACB towards AB
4. Along the bisector of the angle ACB away from AB
Two long straight wires are set parallel to each other. Each carries a current i in the same direction and the separation between them is 2r. The intensity of the magnetic field midway between them is-
1.
2. Zero
3.
4.
The ratio of the magnetic field at the centre of a current-carrying coil of the radius 'a' and at a distance ‘a’ from centre of the coil along the axis of the coil is:
1. 2.
3. 4.
What is the magnetic field at point \(O\) in the figure?

| 1. | \(\dfrac{\mu_{0} I}{4 \pi r}\) | 2. | \(\dfrac{\mu_{0} I}{4 \pi r} + \dfrac{\mu_{0} I}{2 \pi r}\) |
| 3. | \(\dfrac{\mu_{0} I}{4 r} + \dfrac{\mu_{0} I}{4 \pi r}\) | 4. | \(\dfrac{\mu_{0} I}{4 r} - \dfrac{\mu_{0} I}{4 \pi r}\) |
An electron and a proton enter a magnetic field perpendicularly. Both have the same kinetic energy. Which of the following is true:
1. Trajectory of electron is less curved
2. Trajectory of proton is less curved
3. Both trajectories are equally curved
4. Both move on a straight-line path
| 1. | \(\dfrac{\mu _{0}i}{2\pi a}\) | 2. | \(\dfrac{\mu _{0}i\sqrt2}{\pi a}\) |
| 3. | \(\dfrac{2\sqrt2\mu _{0}i}{\pi a}\) | 4. | \(\dfrac{\mu _{0}i}{\sqrt2\pi a}\) |
The magnetic field at the centre of a circular coil of radius r is times that due to a long straight wire at a distance r from it, for equal currents. Figure here shows three cases : in all cases the circular part has radius r and straight ones are infinitely long. For same current the B field at the centre P in cases 1, 2, 3 have the ratio
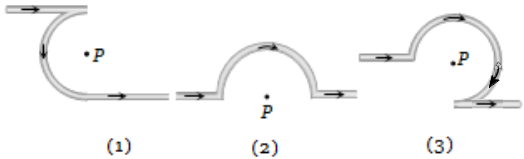
1.
2.
3.
4.
A non-planar loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop is of length 2a. The magnetic field due to this loop at the point P (a,0,a) points in the direction
1.
2.
3.
4.
A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic field vector at a point having coordinates (x, y) in the z = 0 plane is :
1.
2.
3.
4.
| 1. | zero | 2. | \(\dfrac{3\mu_0 i}{32R},~\text{inward}\) |
| 3. | \(\dfrac{3\mu_0 i}{32R},~\text{outward}\) | 4. | \(\dfrac{\mu_0 i}{2R},~\text{inward}\) |