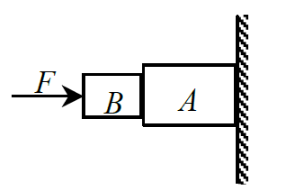
The property of a body by virtue of which it tends to remain in the state of rest or of uniform motion along a straight line is known as:
1. Buoyancy
2. Thrust
3. Inertia
4. Motion
Net force on a body
1. Can increase speed of the body
2. Can decreases speed of the body
3. Can change direction of motion of the body
4. All of these
When a force F is applied on a body of mass m, it creates an acceleration a in the body. If the same force is applied on a body of mass 3 m, then acceleration will be
1.
2.
3.
4.
Action and Reaction forces
1. Cancel each other
2. Acts on same body
3. Always attractive
4. Acts Simultaneously
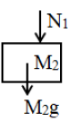
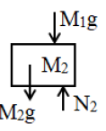
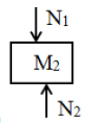
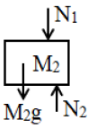
A block A of mass is placed on a block B of mass , which is placed in a table as shown in figure. The correct free body diagram of the block B is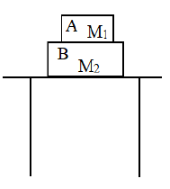
1. 
2. 
3. 
4. 
In the situation shown in figure the value of tension is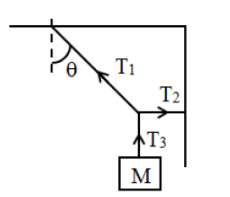
1. Mg
2. Mg sec
3. Mg tan
4. Zero
No force is required
1. To increase momentum
2. To decrease momentum
3. To change direction of momentum
4. To move a body along a straight line
In the situation shown in figure , the tension in the string is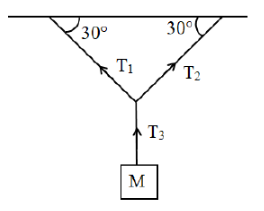
1. Mg
2.
3.
4.
In the situation shown in figure, the Normal reaction exerted by B On C is 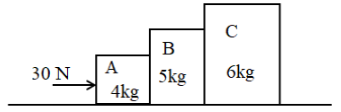
1. 12 N
2. 1O N
3. 18 N
4. 22 N
The tension in the string connecting the two blocks is:
1.
2. f
3.
4.
A pendulum bob is suspended in a Car moving horizontally with acceleration ‘a’ the angle the string will make with vertical is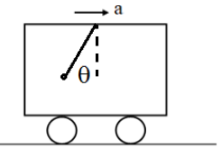
1.
2.
3.
4.
In the situation shown in figure, the value of is
1.
2.
3.
4.
A force of 1 N is that, which can accelerate a body of mass:
1. 2 kg by an acceleration of 2 m/s2
2. 1 kg by an acceleration of 1 m/s2
3. 3 kg by an acceleration of 3 m/s2
4. 4 kg by an acceleration of 4 m/s2
If the situation shown in figure, the acceleration of mass B is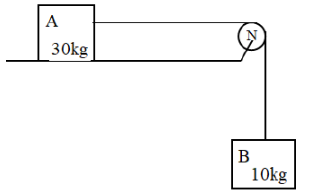
1.
2.
3.
4.
If 3 forces are acting on a body which is at rest, then resultant of any two force must be
1. Zero
2. Equal and opposite to third force
3. Equal and parallel to third force
4. Equal and perpendicular to third force
A balloon of weight W newton descends with an acceleration . The weight that must be thrown out in order to give equal upward acceleration to the Balloon will be
1.
2.
3.
4.
Two blocks and are connected with each other through a light spring as shown in figure. A constant force F acts on in and cause acceleration of a in at an instant. The acceleration of at that instrnt will be
1.
2.
3.
4.
In the arrangement shown, the ends \(P\) and \(Q\) of an inextensible string move downwards with uniform speed \(v.\) The pulleys \(A\) and \(B\) are fixed. The mass \(M\) moves upward with a speed of:
1. \(2 v \cos \theta\)
2. \(v \cos \theta\)
3. \(\left(\frac{2 v}{\cos \theta}\right)\)
4. \(\left(\frac{v}{\cos \theta}\right)\)
The system is pushed by a force F as shown in figure. All surfaces are smooth except between B and C. Friction coefficient between B and C is . Minimuni value of F to prevent block B from slipping is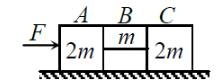
1.
2.
3.
4.
A block of mass is placed on the floor of lift which is moving with velocity = , where is time in second and velocity m/s. Find the time at which normal force on the block is three times of its weight.
1. (3g/8)s
2. g s
3. g/4 s
4. 3g s
In the diagram shown, the shaded pulley has mass 2M. A man of mass M pulls the pulley upwards with constant velocity. If friction is not present between the man and the ground then what will be the acceleration of the man? (Neglect friction between pulley and string)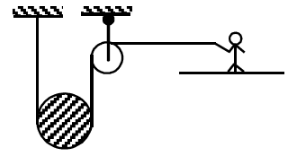
1. 2g
2. 3g/2
3. 2g/3
4. g
All the surfaces shown in figure are smooth. If and are the tension in strings connected to block A and B respectively, then / is (Pulley and strings are ideal) 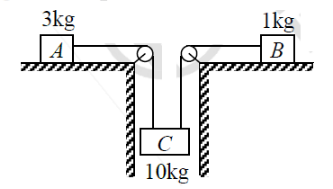
Two masses of 5 kg and 10 kg respectively are connected by a massless spring as shown in the figure. A force of 60 N acts on the 10 kg mass. At the instant shown the 10 kg mass has acceleration 5 . The acceleration of 5 kg mass is-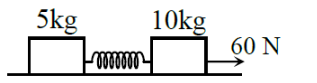
1. 2
2. 4
3. 5
4. 12
A string of negligible mass going over a clamped pulley of mass m support a block of mass Mas shown in the figure. The force on the pulley by the clamp is given by:

1.
2. 2 Mg
3.
4.
Two blocks of masses 2 and are connected as shown in the figure. Now the string between the blocks is suddenly cut. Then, at that instant, accelerations of the blocks A and B will be 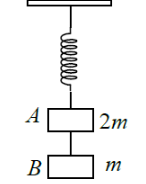
1. g and g, respectively
2. g and g/2, respectively
3. g/2 and g, respectively
4. g/2 and g/2, respectively
Two blocks of masses 2 kg and 5 kg are at rest on ground. The masses are connected by a string passing over a frictionless pulley which is under the influence of a constant upward force F = 50 N. The accelerations of 5 kg and 2 kg masses are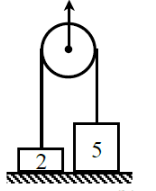
1. 0, 2.5
2. 0,0
3. 2.5 , 2.5
4. 1 , 2.5
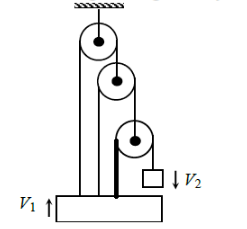
1. \(7v_1-v_2=0\)
2. \(7v_1+v_2=0\)
3. \(v_1+v_2=0\)
4. \(v_1+3v_2=0\)
Using constraint equations relation between and will be 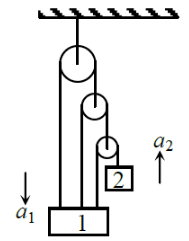
1. =3
2. a =3
3. a= 6
4. a= 7
The acceleration of blocks \(m_1\) and \(m_2\) with respect to the pulley in the condition shown in the figure will be: (pulley and string are ideal. \(g = 10~\text{m/s}^2\))

1. \(10~\text{m/s}^2\)
2. \(5~\text{m/s}^2\)
3. \(\frac{10}{3}~\text{m/s}^2\)
4. zero
A block of mass 2 kg is hanging with two identical massless springs as shown in figure. The acceleration of the block just at the moment, the right spring breaks is (g = 10 )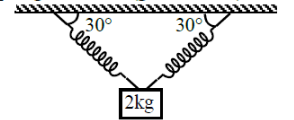
1. 10
2. 25
3. 5
4. 4