Please be patient as the PDF generation may take upto a minute.

A blind person after walking 10 steps in one direction, each of length 80 cm, turns randomly to the left or to the right by $90°.$ After walking a total of 40 steps the maximum possible displacement of the person from his starting position could be -
(1)  $320 \mathrm{m}$
(2)  $32 \mathrm{m}$
(3)  $16/\sqrt{2} \mathrm{m}$
(4)  $16\sqrt{2} \mathrm{m}$

The resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -
                               
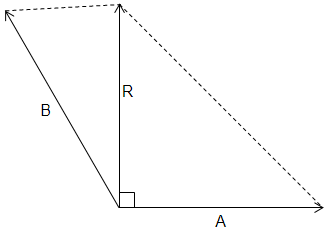
1. $120°$
2.  $150°$
3.  $135°$
4.  None of these

A particle is moving in a circle of radius r centered at O with constant speed v. The change in velocity moving from A to B $\left(\angle \mathrm{AOB}=40°\right)$ is -
(A)  $2\mathrm{v} \cos 40°$
(B)  $2\mathrm{v} \sin 40°$
(C)  $2\mathrm{v} \cos 20°$
(D)  $2\mathrm{v} \sin 20°$

The value of unit vector in the direction of vector $\mathrm{A}=5 \hat{\mathrm{i}}-12 \hat{\mathrm{j}}$, is -
1. $\hat{\mathrm{i}}$
2. $\hat{\mathrm{j}}$
3. $\left(\hat{\mathrm{i}}+\hat{\mathrm{j}}\right)/13$
4. $\left(5\hat{\mathrm{i}}-12\hat{\mathrm{j}}\right)/13$

A child pulls a box with a force of \(200~\text{N}\) at an angle of $\mathrm{}$\(60^{\circ}\) above the horizontal. Then the horizontal and vertical components of the force will be:
              
1. \(100~\text{N}, ~175~\text{N}\)
2. \(86.6~\text{N}, ~100~\text{N}\)
3. \(100~\text{N}, ~86.6~\text{N}\)
4. \(100~\text{N}, ~0~\text{N}\)

A man rows a boat at a speed of $\mathrm{}$\(18~\text{km/hr}\) in the northwest direction. The shoreline makes an angle of $\mathrm{}$\(15^{\circ}\) south of west. The component of the velocity of the boat along the shoreline is:
1. \(9~\text{km/hr}\)
2. \(18\frac{\sqrt{3}}{2}~\text{km/hr}\)
3. \(18\cos 15^{\circ}~\text{km/hr}\)
4. \(18\cos 75^{\circ}~\text{km/hr}\)

A bird moves from point (1, -2) to (4, 2). If the speed of the bird is 10 m/sec, then the velocity vector of the bird is:
1. $5\left(\hat{\mathrm{i}}-2\hat{\mathrm{j}}\right)$
2. $5\left(4\hat{\mathrm{i}}+2\hat{\mathrm{j}}\right)$
3. $0.6\hat{\mathrm{i}}+0.8\hat{\mathrm{j}}$
4. $6\hat{\mathrm{i}}+8\hat{\mathrm{j}}$

If the angle between the unit vectors $\hat{\mathrm{a}}$ and $\hat{\mathrm{b}}$ is $60°$, then $|\hat{\mathrm{a}}-\hat{\mathrm{b}}|$ is :
(1)  0
(2)  1
(3)  2
(4)  4

Two constant forces ${\overrightarrow{\mathrm{F}}}_1=2\hat{\mathrm{i}}-3\hat{\mathrm{j}}+3\hat{\mathrm{k}} \left(\mathrm{N}\right)$ and ${\overrightarrow{\mathrm{F}}}_2=\hat{\mathrm{i}}+\hat{\mathrm{j}}-2\hat{\mathrm{k}} \left(\mathrm{N}\right)$ act on a body and displace it from the position ${\overrightarrow{\mathrm{r}}}_1=\hat{\mathrm{i}}+2\hat{\mathrm{j}}-2\hat{\mathrm{k}} \left(\mathrm{m}\right)$ to the position ${\overrightarrow{\mathrm{r}}}_2=7\hat{\mathrm{i}}+10\hat{\mathrm{j}}+5\hat{\mathrm{k}} \left(\mathrm{m}\right)$. What is the work done W? $[Given : W =\overrightarrow{F}.∆\overrightarrow{r}]$
(A)  9 Joule
(B)  41 Joule
(C)  -3 Joule
(D)  None of these

The two vectors $\mathrm{A}=2\hat{\mathrm{i}}+\hat{\mathrm{j}}+3\hat{\mathrm{k}}$ and $\mathrm{B}=7\hat{\mathrm{i}}-5\hat{\mathrm{j}}-3\hat{\mathrm{k}}$ are -
1.  parallel
2.  perpendicular
3.  anti-parallel
4.  None of these

The angle that the vector $\mathrm{A}=2\hat{\mathrm{i}}+3\hat{\mathrm{j}}$ makes with the y-axis is:
(1)  ${\tan }^{-1} 3/2$
(2)  ${\tan }^{-1} 2/3$
(3)  ${\sin }^{-1} 2/3$
(4)  ${\cos }^{-1} 3/2$

The linear velocity of a rotating body is given by $\overrightarrow{\mathrm{v}}=\overrightarrow{\mathrm{\omega }}\times \overrightarrow{\mathrm{r}}$, where $\mathrm{\omega }$ is the angular velocity and r is the radius vector. The angular velocity of a body, $\overrightarrow{\mathrm{\omega }}=\hat{\mathrm{i}}-2\hat{\mathrm{j}}+2\hat{\mathrm{k}}$ and their radius vector is  $\overrightarrow{\mathrm{r}}=4\hat{\mathrm{j}}-3\hat{\mathrm{k}}, \mathrm{then\; value\; of} \left|\overrightarrow{\mathrm{v}}\right|$ will be:
1. $\sqrt{29} \mathrm{units}$
2. $31 \mathrm{units}$
3. $\sqrt{37} \mathrm{units}$
4. $\sqrt{41} \mathrm{units}$

A vector $\overrightarrow{\mathrm{A}}$ is directed along $30°$ west of north direction and another vector $\overrightarrow{\mathrm{B}}$ along $15°$ south of east. Their resultant cannot be in ____________ direction.
(1)  North
(2)  East
(3)  North-East
(4)  South

ABCD is a quadrilateral. Forces $\overrightarrow{\mathrm{BA}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}} \& \overrightarrow{\mathrm{DA}}$ act at a point. Their resultant is 
(A)  $2 \overrightarrow{\mathrm{AB}}$
(B)  $2 \overrightarrow{\mathrm{DA}}$
(C)  zero vector
(D)  $2 \overrightarrow{\mathrm{BA}}$

The resultant of the forces \(\overrightarrow {P}\) and \(\overrightarrow {Q}\) is \(\overrightarrow {R}\). If \(\overrightarrow {Q}\) is doubled, then the resultant also doubles in magnitude. Find the angle between \(\overrightarrow {P}\) and \(\overrightarrow {Q}\)?
1. \(\cos\theta = \frac{Q}{2P}\)
2. \(\cos\theta = \frac{-4Q}{3P}\)
3. \(\cos\theta = \frac{-2Q}{3P}\)
4. \(\cos\theta = \frac{-3P}{4Q}\)

The maximum and minimum magnitude of the resultant of two vectors are 17 units and 7 units respectively. Then the magnitude of resultant of the vectors when they act perpendicular to each other is:
(1)  14
(2)  16
(3)  18
(4)  13

A vector $\overrightarrow{\mathrm{A}}$ makes an angle of $20°$ and $\overrightarrow{\mathrm{B}}$ makes an angle of $110°$ with the X-axis. The magnitudes of these vectors are 3 m and 4 m respectively. Find the magnitude of the resultant.
(A)  $1$
(B)  $5\sqrt{2}$
(C)  $5$
(D)  $7$

A particle is moving westward with a velocity ${\overrightarrow{\mathrm{v}}}_i=5 \mathrm{m}/\mathrm{s}.$ Its velocity changed to ${\overrightarrow{\mathrm{v}}}_f=5\mathrm{m}/\mathrm{s}$ northward. The change in velocity vector $\left(∆\overrightarrow{\mathrm{V}}={\overrightarrow{\mathrm{v}}}_f-{\overrightarrow{\mathrm{v}}}_i\right)$ is:
(1)  $5\sqrt{2} \mathrm{m}/\mathrm{s}$ towards north east
(2)  $5 \mathrm{m}/\mathrm{s}$ towards north west
(3)  zero
(4)  $5\sqrt{2} \mathrm{m}/\mathrm{s}$towards north west

Consider east as positive x-axis, north as positive y-axis and vertically upward direction as z-axis. A helicopter first rises up to an altitude of 100 m than flies straight in north 500 m and then suddenly takes a turn towards east and travels 1000 m east. What is position vector of helicopter. (Take starting point as origin)
(1)  $1000 \hat{\mathrm{i}}-500 \hat{\mathrm{j}}+100 \hat{\mathrm{k}}$
(2)  $1000 \hat{\mathrm{i}}+500 \hat{\mathrm{j}}-100 \hat{\mathrm{k}}$
(3)  $1000 \hat{\mathrm{i}}+500 \hat{\mathrm{j}}+100 \hat{\mathrm{k}}$
(4)  $-1000 \hat{\mathrm{i}}+500 \hat{\mathrm{j}}+100 \hat{\mathrm{k}}$

$\overrightarrow{\mathrm{A}}=\hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}; \overrightarrow{\mathrm{B}}=2\hat{\mathrm{i}}+3\hat{\mathrm{j}}+5\hat{\mathrm{k}}$, then angle between $\overrightarrow{\mathrm{A}}$ and $\overrightarrow{\mathrm{B}}$ is:
(A)  $120°$
(B)  $90°$
(C)  $60°$
(D)  $30°$

Given the vectors
$\overrightarrow{\mathrm{A}}=2\hat{\mathrm{i}}+3\hat{\mathrm{j}}-\hat{\mathrm{k}}$
$\overrightarrow{\mathrm{B}}=3\hat{\mathrm{i}}-2\hat{\mathrm{j}}-2\hat{\mathrm{k}}$
$\& \overrightarrow{\mathrm{C}}=\mathrm{p}\hat{\mathrm{i}}+\mathrm{p}\hat{\mathrm{j}}+2\mathrm{p}\hat{\mathrm{k}}$
Find the angle between $\left(\overrightarrow{\mathrm{A}}-\overrightarrow{\mathrm{B}}\right) \& \overrightarrow{\mathrm{C}}$
(A)  $\mathrm{\theta }={\cos }^{-1}\left(\frac{2}{\sqrt{3}}\right)$
(B)  $\mathrm{\theta }={\cos }^{-1}\left(\frac{\sqrt{3}}{2}\right)$
(C)  $\mathrm{\theta }={\cos }^{-1}\left(\frac{\sqrt{2}}{3}\right)$
(D)  none of these

If vector $\overrightarrow{\mathrm{P}}, \overrightarrow{\mathrm{Q}}$ and $\overrightarrow{\mathrm{R}}$ have magnitude 5, 12 and 13 units and $\overrightarrow{\mathrm{P}}+\overrightarrow{\mathrm{Q}}=\overrightarrow{\mathrm{R}}$, then the angle between $\overrightarrow{\mathrm{Q}}$ and $\overrightarrow{\mathrm{R}}$ will be:
1.  ${\cos }^{-1} \frac{5}{12}$
2.  ${\cos }^{-1} \frac{5}{13}$
3.  ${\cos }^{-1} \frac{12}{13}$
4.  ${\cos }^{-1} \frac{2}{13}$

The vector having a magnitude of 10 and perpendicular to the vector $3\hat{\mathrm{i}}-4\hat{\mathrm{j}}$ is- 
1. $4\hat{\mathrm{i}}-3\hat{\mathrm{j}}$
2. $5\sqrt{2} \hat{\mathrm{i}}-5\sqrt{2} \hat{\mathrm{j}}$
3. $8\hat{\mathrm{i}}+6\hat{\mathrm{j}}$
4.  $8\hat{\mathrm{i}}-6\hat{\mathrm{j}}$

A force $\overrightarrow{\mathrm{F}}=3\hat{\mathrm{i}}+\mathrm{c}\hat{\mathrm{j}}+2\hat{\mathrm{k}}$ acting on a particle causes a displacement $\overrightarrow{\mathrm{d}}=-4\hat{\mathrm{i}}+2\hat{\mathrm{j}}+3\hat{\mathrm{k}}$. If the work done is 6J then the value of 'c' is- $[Given: W=\overrightarrow{F.}\overrightarrow{d}]$
1. 12 
2. 0
3. 6
4. 1

The x and y components of vector $\overrightarrow{\mathrm{A}}$ are 4m and 6m respectively. The x, y components of vector $\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}$ are 10m and 9m respectively. The length of $\overrightarrow{\mathrm{B}}$ is ______ and angle that $\overrightarrow{\mathrm{B}}$ makes with the x axis is given by _______.
(A)  $\sqrt{0.45}\mathrm{m}, {\tan }^{-1}\left(1/2\right)$
(B)  $\sqrt{4.5}\mathrm{m}, {\tan }^{-1}\left(1/2\right)$
(C)  $\sqrt{45}\mathrm{m}, {\tan }^{-1}\left(1/2\right)$
(D)  $4\sqrt{5}\mathrm{m}, {\tan }^{-1}\left(1/2\right)$

A particle travels with speed 50 m/s from the point (3, 7) in a direction $7\hat{\mathrm{i}}-24\hat{\mathrm{j}}$. Find its position vector after 3 seconds.
1.  $151\hat{\mathrm{i}}+45\hat{\mathrm{j}}$
2.  $45\hat{\mathrm{i}}-137\hat{\mathrm{j}}$
3.  $151\hat{\mathrm{i}}-45\hat{\mathrm{j}}$
4.  $4.5\hat{\mathrm{i}}-151\hat{\mathrm{j}}$

If \(\overrightarrow{A}={2}\hat{i}+\hat{j}\;{\&}\;\overrightarrow{B}=\hat{i}{-}\hat{j},\)  then the components of \(\overrightarrow {A}\) along with \(\overrightarrow {B}\) & perpendicular to \(\overrightarrow {B}\) respectively will be:
1. \(\frac{\hat{i} - \hat{j}}{2} ,~\frac{3}{2}\left(\hat i+\hat j\right)\)
2. \(\frac{\hat{i} - \hat{j}}{2} ,~-\frac{2}{3}\left(\hat i+\hat j\right)\)
3. \(\frac{\hat{i} - \hat{j}}{2} ,~-\frac{3}{2}\left(\hat i-\hat j\right)\)
4. \(\frac{\hat{i} - \hat{j}}{2} ,~\frac{2}{3}\left(\hat i-\hat j\right)\)

If \(\overrightarrow{a}\) is a vector and \(x\) is a non-zero scalar, then which of the following is correct?

A vector that is perpendicular to both the vectors $\overrightarrow{\mathrm{a}}=\hat{\mathrm{i}}-2\hat{\mathrm{j}}+\hat{\mathrm{k}}$ and $\overrightarrow{\mathrm{b}}=\hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}$ is
(A)  $-\hat{\mathrm{i}}+\hat{\mathrm{k}}$
(B)  $-\hat{\mathrm{i}}-2\hat{\mathrm{j}}+\hat{\mathrm{k}}$
(C)  $\hat{\mathrm{i}}-2\hat{\mathrm{j}}+\hat{\mathrm{k}}$
(D)  $\hat{\mathrm{i}}+\hat{\mathrm{k}}$

If \(\theta\) is the angle between two vectors $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$, and $|\overrightarrow{\mathrm{a}}\times \overrightarrow{\mathrm{b}}|=\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}$, then \(\theta\) is equal to:
1. \(0^\circ\)
2. \(180^\circ\)
3. \(135^\circ\)
4. \(45^\circ\)

The vector \(\overrightarrow b\) which is collinear with the vector \(\overrightarrow a = \left(2, 1, -1\right)\) and satisfies the condition \(\overrightarrow a. \overrightarrow b=3\) is:
1. \(\left(1, \frac{1}{2}, \frac{-1}{2}\right)\)
2. \(\left(\frac{2}{3}, \frac{1}{3}, \frac{-1}{3}\right)\)
3. \(\left(\frac{1}{2}, \frac{1}{4}, \frac{-1}{4}\right)\)
4. \(\left(1, 1, 0\right)\)

If a vector $\left(2\hat{\mathrm{i}}+3\hat{\mathrm{j}}+8\hat{\mathrm{k}}\right)$ is perpendicular to the vector $\left(4\hat{\mathrm{i}}-4\hat{\mathrm{j}}+\mathrm{\alpha }\hat{\mathrm{k}}\right)$. Then the value of $\mathrm{\alpha }$ is:
1.  -1
2.  1/2
3.  -5/2
4.  1

If a, b and c are three non-zero vectors such that $\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}=0$, then the value of $\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}}.\overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{c}}.\overrightarrow{\mathrm{a}}$ will be:

Let $\mathrm{\alpha }, \mathrm{\beta }, \mathrm{\gamma }$ be distinct real numbers. The points with position vectors $\mathrm{\alpha }\hat{\mathrm{i}}+\mathrm{\beta }\hat{\mathrm{j}}+\mathrm{\gamma }\hat{\mathrm{k}} , \mathrm{\beta }\hat{\mathrm{i}}+\mathrm{\gamma }\hat{\mathrm{j}}+\mathrm{\alpha }\hat{\mathrm{k}} , \mathrm{\gamma }\hat{\mathrm{i}}+\mathrm{\alpha }\hat{\mathrm{j}}+\mathrm{\beta }\hat{\mathrm{k}}$
(1)  are collinear
(2)  from an equilateral triangle
(3) form an isosceles triangle
(4)  from a right angled triangle

Two vectors $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$ inclined at an angle $\mathrm{\theta }$ with respect to each other have a resultant $\overrightarrow{\mathrm{c}}$ which makes an angle $\mathrm{\beta }$ with $\overrightarrow{\mathrm{a}}$. If the directions of $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$ are interchanged, then the resultant will have the same
(A)  magnitude
(B)  direction
(C)  magnitude as well as direction
(D)  neither magnitude nor direction

Two vectors $\overrightarrow{\mathrm{A}}$ and $\overrightarrow{\mathrm{B}}$ lie in a plane. Another vector $\overrightarrow{\mathrm{C}}$ lies outside this plane. The resultant $\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{C}}$ of these three vectors
(1)  can be zero
(2)  cannot be zero
(3)  lies in the plane of $\overrightarrow{\mathrm{A}} \&\overrightarrow{\mathrm{B}}$
(4)  lies in the plane of $\overrightarrow{\mathrm{A}} \& \overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}$

A set of vectors taken in a given order gives a closed polygon. Then the resultant of these vectors is a 
(1)  scalar quantity
(2)  pseudovector
(3)  unit vector
(4)  null vector

Component of $3\hat{i}+4\hat{j}$ perpendicular to $\hat{i}+\hat{j}$ and in the same plane as that of $3\hat{i}+4\hat{j}$ is:
1.  $\frac{1}{2}\left(\hat{j}-\hat{i}\right)$
2.  $\frac{3}{2}\left(\hat{j}-\hat{i}\right)$
3.  $\frac{5}{2}\left(\hat{j}-\hat{i}\right)$
4.  $\frac{7}{2}\left(\hat{j}-\hat{i}\right)$

Given that $\overrightarrow{\mathrm{C} }= \overrightarrow{A } + \overrightarrow{B } \mathrm{and} \overrightarrow{\mathrm{C} }$ makes an angle $\mathrm{\alpha } \mathrm{with} \overrightarrow{\mathrm{A}} \mathrm{and} \mathrm{\beta } \mathrm{with} \overrightarrow{\mathrm{B}}$. Which of the following options is correct?
1.  $\mathrm{\alpha } \mathrm{cannot} \mathrm{be} \mathrm{less} \mathrm{then} \mathrm{\beta }$
2.  $\mathrm{\alpha } <\mathrm{\beta }, \mathrm{if} \mathrm{A}<\mathrm{B}$
3.  $\mathrm{\alpha } <\mathrm{\beta }, \mathrm{if} \mathrm{A}>\mathrm{B}$
4.  $\mathrm{\alpha } <\mathrm{\beta }, \mathrm{if} \mathrm{A}=\mathrm{B}$

If the angle between the vector $\overrightarrow{\mathrm{A}} \mathrm{and} \overrightarrow{\mathrm{B}} is \mathrm{\theta }$, the value of the product $\left(\overrightarrow{B}\times \overrightarrow{A}\right). \overrightarrow{A}$ is equal to :
1.  $B{A}^2$ cos$\theta$
2.  $B{A}^2$ sin$\theta$
3.  $B{A}^2$ sin$\theta$ cos$\theta$
4.  zero

Two forces A and B have a resultant $R_1$. If B is doubled, the new resultant $R_2$ is perpendicular to A. Then
1.  $R_1$ = A
2.  $R_1$ = B
3.  $R_2$ = A
4.  $R_2$ = B 

A force of 6 N and another of 8 N can be applied together to produce the effect of a single force of -
1.  1 N
2.  11 N
3.  15 N
4.  20 N

Which of the sets given below may represent the magnitudes of three vectors adding to zero?
(A)  2, 4, 8
(B)  4, 8, 16
(C)  1, 2, 1
(D)  0.5, 1, 2