Please be patient as the PDF generation may take upto a minute.

1.

The elastic energy stored in a wire of Young's Modulus Y is -
1. $\mathrm{Y}\times \frac{{\mathrm{strain}}^2}{\mathrm{volume}}$
2. $\mathrm{stress}\times \mathrm{strain}\times \mathrm{volume}$
3. $\frac{{\mathrm{strain}}^2\times \mathrm{volume}}{2\mathrm{Y}}$
4. $\frac{1}{2}\times stress\times strain\times volume$

2.

If a spring of spring constant k is stretched by a length x under tension T, the energy stored is 
1. $\frac{2k}{T^2}$
2. $\frac{2T^2}{k}$
3. $\frac{T^2}{2k}$
4. $\frac{2T}{k^2}$

3.

In steel, the Young's modulus and the strain at the breaking point are $2\times {10}^{11}N{m}^{-2}$ and 0.15 respectively. The stress at the breaking point for steel is therefore -
1. $1.33\times {10}^{11}N{m}^{-2}$           
2. $1.33\times {10}^{12}N{m}^{-2}$
3. $7.5\times {10}^{-13}N{m}^{-2}$           
4. $3\times {10}^{10}N{m}^{-2}$

4.

An iron rod of length 2m and cross section area of 50 X ${10}^{-6} m^2$ , is stretched by 0.5 mm, when a mass of 250 kg is hung from its lower end. Young's modulus of the iron rod is-
1. $19.6\times {10}^{10}N/m^2$                         
2. $19.6\times {10}^{15}N/m^2$
3. $19.6\times {10}^{18}N/m^2$                         
4. $19.6\times {10}^{20}N/m^2$

5.

If a rubber ball is taken at the depth of 200 m in a pool, its volume decreases by 0.1%. If the density of the water is $1\times {10}^{3}kg/m^3$ and $g=10m/s^2$, then the volume elasticity in  will be
1. ${10}^8$                                       
2. $2\times {10}^8$
3. ${10}^9$                                         
4. $2\times {10}^9$

6.

Shearing stress causes a change in-
1.   Length                              
2.   Breadth
3.   Shape                               
4.   Volume

7.

The adjacent graph shows the extension $\left(∆l\right)$ of a wire of length 1m suspended from the top of a roof at one end with a load W connected to the other end. If the cross sectional area of the wire is ${10}^{-6}{m}^2$ calculate the young’s modulus of the material of the wire

1. $2\times {10}^{11}N/m^2$
2. $2\times {10}^{-11}N/m^2$
3. $3\times {10}^{-12}N/m^2$
4. $2\times {10}^{-13}N/m^2$

8.

A wire can sustain a weight of 10 kg before breaking. If the wire is cut into two equal parts, then each part can sustain a weight of:

1.	2.5 kg	2.	5 kg
3.	10 kg	4.	15 kg

9.

The stress-strain curves are drawn for two different materials \(X\) and \(Y.\) It is observed that the ultimate strength point and the fracture point are close to each other for material \(X\) but are far apart for material \(Y.\) We can say that the materials \(X\) and \(Y\) are likely to be (respectively):

1.	ductile and brittle
2.	brittle and ductile
3.	brittle and plastic
4.	plastic and ductile

10.

A man grows into a giant such that his linear dimensions increase by a factor of 9. Assuming that his density remains the same, the stress in the leg will change by a factor of:
1.  $\frac{1}{81}$
2.  9
3.  $\frac{1}{9}$
4.  81

11. Given below are two statements: 

Statement I:	Air is more elastic than iron.
Statement II:	Elasticity is directly proportional to Bulk modulus.

1.	Statement I is false but Statement II is true.
2.	Both Statement I and Statement II are true.
3.	Both Statement I and Statement II are false.
4.	Statement I is true but Statement II is false.

12. Breaking stress of a wire of length \(L\) and radius \(r\) is \(B\). If another wire made of the same material has length \(2L\) and radius \(2r\), its breaking stress will be:
1. \(2B\)
2. \(\frac{B}{4}\)
3. \(B\)
4. \(4B\)

13.

Two wires of the same material have lengths in the ratio of 1: 2. If they are stretched by applying equal forces, the increase in lengths is the same. The ratio of their respective radii is:
(1) 1: 1
(2) 1: 2
(3) 1: $\sqrt{2}$
(4) 2: 1

14.

When a mass M is suspended by a wire, it elongates the wire by length l. The work done during this elongation process is:
(1) Zero
(2) $\frac{1}{2}$Mgl
(3) Mgl
(4) 2Mgl

15.

Given that the breaking stress of a wire is 7.2 x ${10}^7$ N/ ${\mathrm{m}}^2$ and its density is 7.2 g/cc, then the maximum length of the wire which can hang without breaking is: (g = 10 m/${\mathrm{s}}^2$)
(1) 1000 m
(2) 100 m
(3) 200 m
(4) 50 m

16.

Select the incorrect statement about Bulk modulus of elasticity.
(1) It is defined for solids, liquids and gases.
(2) ${\mathrm{B}}_{\mathrm{solid}} > {\mathrm{B}}_{\mathrm{liquid}} > {\mathrm{B}}_{\mathrm{gas}}$
(3) The bulk modulus of gas is different for different processes.
(4) Almost for all materials, the Bulk modulus increases with the rise in temperature.

17.

A uniform rod suspended from the ceiling gets elongated by its weight. Which one of the following graphs represents the variation of elongation with length, \(L\)?

1.		2.
3.		4.

18.

The maximum load that a wire can bear is W. If the wire is cut to half of its length, then the maximum load it can sustain is:
1.  $\frac{\mathrm{W}}{4}$
2.  $\frac{\mathrm{W}}{3}$
3.  $\frac{\mathrm{W}}{2}$
4.  W

19.

If a wire is stretched to double its original length, then the strain in the wire is:
1. \(1\)
2. \(2\)
3. \(3\)
4. \(4\)

20.

Anvils made of single crystals of diamond, with the shape as shown in the figure, are used to investigate the behaviour of materials under very high pressures. Flat faces at the narrow end of the anvil have a diameter of \(0.50\) mm, and the wide ends are subjected to a compressional force of \(50,000\) N. What is the pressure at the tip of the anvil?

1. \(2.5\times10^{11}\) Pa
2. \(3.7\times10^{11}\) Pa
3. \(2.1\times10^{11}\) Pa
4. \(1.9\times10^{11}\) Pa
${\mathrm{}}^{}$

21.

The figure shows the graph between stress and strain for a uniform wire at two different temperatures. Then: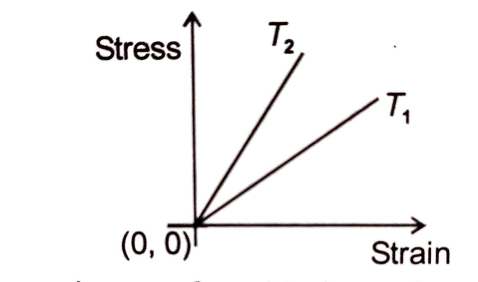

1. \(T_1>T_2\)
2. \(T_2>T_1\)
3. \(T_1=T_2\)
4. None of these

22.

On stretching some substances, why is permanent elongation caused?
1. They are perfectly elastic.
2. They are perfectly plastic.
3. More stress acts on them.
4. Their strain is infinite.

23. The modulus of rigidity of the ideal liquid is:
1. infinity
2. zero
3. unity
4. some finite small non-zero constant value

24.

A rope \(1\) cm in diameter breaks if the tension in it exceeds \(500\) N. The maximum tension that may be given to a similar rope of diameter \(2\) cm is:
1. \(500\) N
2. \(250\) N
3. \(1000\) N
4. \(2000\) N

25.

A wire elongates by \(1.0\) mm when a load \(W\) is hang from it. If this wire goes over a pulley and two weights \(W\) each are hung at the two ends, the elongation of the wire will be:
1. \(0.5\) m
2. \(1.0\) mm
3. \(2.0\) mm
4. \(4.0\) mm

26.

A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break:

1.	when the mass is at the highest point
2.	when the mass is at the lowest point
3.	when the wire is horizontal
4.	at an angle of \(\cos^{-1}\left(\frac{1}{3}\right)\) from the upward vertical

27. A material like rubber which can be stretched to cause large strain is called:
1. highly elastic
2. ductile
3. plastic
4. elastomers

28. Three identical \(4~\text{kg}\) blocks are placed one atop of the other, as shown in the figure, on a smooth horizontal plane. The system is placed in an elevator moving upward with an acceleration equal to \(g.\) Consider the three horizontal surfaces of contact ①, ②, ③, all of these having the same cross-sectional area. Let, the stresses at these surfaces be \(S_1,S_2,S_3.\) Then:

Statement I:	\(S_1,S_2,S_3\) increase when the elevator is accelerated upward.
Statement II:	The proportion \(S_1:S_2:S_3\) remains unchanged with acceleration.

 

1.	Statement I is incorrect and Statement II is correct.
2.	Both Statement I and Statement II are correct.
3.	Both Statement I and Statement II are incorrect.
4.	Statement I is correct and Statement II is incorrect.

29. If in a wire of Young's modulus \(Y\), longitudinal strain \(X\) is produced, then the value of potential stored in its unit volume will be: 
1. \(Y X^2\)
2. \(2 Y X^2\)
3. \(\frac{Y^2 X}{2} \)
4. \(\frac{Y X^2}{2}\)

30. A block of iron of volume \(V_0\) (in air) is taken to a depth \(x\) under the sea (assume that the density of sea-water is constant). The volume of this block decreases by \(\Delta V\) due to pressure of sea-water. Then, \(\Delta V\) is proportional to:

1.	\(x\)	2.	\(x^2\)
3.	\(x^3\)	4.	\(x^{-3}\)