Please be patient as the PDF generation may take upto a minute.

A spring 40 mm long is stretched by the application of a force. If 10 N force required to stretch the spring through 1 mm, then work done in stretching the spring through 40 mm is
1. 84J
2. 68J
3. 23J
4. 8J

A particle is moving on the circular path of the radius (R) with centripetal acceleration $a_c=k^{2}R{t}^2$. Then the correct relation showing power (P) delivered by net force versus time (t) is 

1. 1
2. 2
3. 3
4. 4

A body is displaced from (0,0) to (1m,1m) along the path x=y by a force $F=\left(x^2\hat{j}+y\hat{i}\right)N$. The work done by this force will be :
1. $\frac{4}{3}J$
2. $\frac{5}{6}J$
3. $\frac{3}{2}J$
4. $\frac{7}{5}J$

A weightless rod of length 2l carries two equal mass 'm', one tied at lower end A and the other at the middle of the rod at B. The rod can rotate in a vertical plane about a fixed horizontal axis passing through C. The rod is released from rest in the horizontal position. The speed of the mass B at the instant rod becomes vertical is:

1. \(\sqrt{\frac{3 g l}{5}} \)
2. \(\sqrt{\frac{4 g l}{5}} \)
3. \(\sqrt{\frac{6 g l}{5}} \)
4. \(\sqrt{\frac{7 g l}{5}} \)

As per the given figure to complete the circular loop, what should be the radius of the loop?
 
 
1. 4 m
2. 3 m
3. 2.5 m
4. 2 m

A force acts on a 30 gm particle in such a way that the position of the particle as a function of time is given by $x=3t-4t^2+t^3$, where x is in metres and t is in seconds. The work done during the first 4 seconds is 
(1) 5.28 J
(2) 450 mJ
(3) 490 mJ
(4) 530 mJ

A particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to- 
(1) x²
(2) e^x
(3) x
(4) log_e x

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k. The maximum compression in the spring is x then-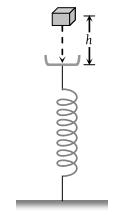

(1) $mgh=\frac{1}{2}k{x}^2$
(2) $mg(h+x)=\frac{1}{2}k{x}^2$
(3) $mgh=\frac{1}{2}k{(x+h)}^2$
(4) $mg(h+x)=\frac{1}{2}k{(x+h)}^2$

An open knife edge of mass 'm' is dropped from a height 'h' on a wooden floor. If the blade penetrates upto the depth 'd' into the wood, the average resistance offered by the wood to the knife edge is 
(1) mg
(2) $mg\left(1-\frac{{\displaystyle h}}{{\displaystyle d}}\right)$
(3) $mg\left(1+\frac{{\displaystyle h}}{{\displaystyle d}}\right)$
(4) $mg{\left(1+\frac{{\displaystyle h}}{{\displaystyle d}}\right)}^2$

The force acting on a body moving along x-axis varies with the position of the particle as shown in the fig.

The body is in stable equilibrium at
(1) x = x₁
(2) x = x₂
(3) both x₁ and x₂
(4) neither x₁ nor x₂

A ball is thrown vertically downwards from a height of 20 m with an initial velocity v_o. It collides with the ground, loses 50% of its energy in a collision and rebounds to the same height. The initial velocity v_o is: (Take g = 10 ms^-2)
1. 14 ms^-1
2. 20 ms^-1
3. 28 ms^-1
4. 10 ms^-1

The potential energy of a system increases if work is done
(1) by the system against a conservative force 
(2) by the system against a nonconservative force
(3) upon the system by a conservative force
(4) upon the system by a nonconservative force

The points of maximum and minimum attraction in the curve between potential energy (U) and distance (r) of a diatomic molecules are respectively -

(1) S and R
(2) T and S
(3) R and S
(4) S and T

Two balls having different masses are moving towards each other with speed 30 m/s and 20 m/s as shown in figure (i). Their velocities after collision become 20 m/s and 30 m/s as shown in the figure (ii), then the coefficient of restitution is: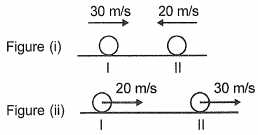

(1)  1
(2)  0.5
(3)  0.4
(4)  0.2

A smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision, their final velocities are V and v respectively. The value of v is:-
1. $\frac{2\mathrm{uM}}{\mathrm{m}}$
2. $\frac{2\mathrm{um}}{\mathrm{M}}$
3. $\frac{2\mathrm{u}}{1+{\displaystyle \frac{\mathrm{m}}{\mathrm{M}}}}$
4. $\frac{2\mathrm{u}}{1+{\displaystyle \frac{\mathrm{M}}{\mathrm{m}}}}$