Please be patient as the PDF generation may take upto a minute.

Find $t_5 and t_6$ of the arithmetic progression 0, $\frac{1}{4}, \frac{1}{2}, \frac{3}{4}, ...$
1.  $1, \frac{5}{4}$
2.  $\frac{5}{4}, 1$
3.  $1, \frac{7}{4}$
4.  $\frac{7}{4}, 1$

$\mathrm{If} {\mathrm{t}}_{\mathrm{n}} = 6\mathrm{n} + 5, \mathrm{then} {\mathrm{t}}_{\mathrm{n} + 1} = \mathrm{\_\_\_\_\_\_\_\_\_\_\_} .$
1.  $6n - 1$
2.  $6n + 11$
3.  $6n + 6$
4.  $6n - 5$

Which term of the arithmetic progression 21, 42, 63, 84, .... is 420
1.  19
2.  20
3.  21
4.  22

Find the 15th term of the arithmetic progression 10, 4, -2, ...
1.  -72
2.  -74
3.  -76
4.  -78

If the kth term of the arithmetic progression 25, 50, 75, 100, ... is 1000, then k is _________ .
1.  20
2.  30
3.  40
4.  50

The sum of the first 20 terms of an arithmetic progression whose first term is 5 and common difference is 4, is ___________ .
1.  820
2.  830
3.  850
4.  860

Two arithmetic progression have equal common differences. The first term of one of these is 3 and that of the other is 8, then the difference between their 100th terms is _____________ .
1.  4
2.  5
3.  6
4.  3

If, a, b and c are in arithmetic progression, then b + c, c + a and a + b are in
1.  arithmetic progression
2.  geometric progression
3.  harmonic progression
4.  none of these

The sum of the first 51 term of the arithmetic progression whose 2nd term is 2 and 4th term is 8, is ____________ .
1.  3774
2.  3477
3.  7548
4.  7485
 

$\mathrm{If} {\mathrm{t}}_{\mathrm{n}} = 3^{\mathrm{n} - 1}, \mathrm{then} {\mathrm{s}}_6 - {\mathrm{s}}_5 = \mathrm{\_\_\_\_\_\_\_\_\_} .$
1.  243
2.  81
3.  77
4.  27

Find the 15th term of the series 243, 81, 27, ....
1.  $\frac{1}{3^{14}}$
2.  $\frac{1}{3^8}$
3.  ${\left(\frac{1}{3}\right)}^9$
4.  ${\left(\frac{1}{3}\right)}^{10}$

If the 3rd, 7th and 11th term of a geometric progression and p, q and r is __________.
1.  $p^2 = qr$
2.  $r^2 = qp$
3.  $q^2 = p^{2r2}$
4.  $q^2 = pr$

Find the sum of the first 10 terms os geometric progression 18, 9, 4.5, ...
1.  $9\frac{\left(2^{10} - 1\right)}{2^8}$
2.  $9\frac{\left(2^{10} - 1\right)}{2^{10}}$
3.  $36\frac{\left(2^{10} - 1\right)}{2^8}$
4.  $8\frac{\left(2^{10} - 1\right)}{2^8}$

$Evaluate \sum _{}^{}(3 + 2^r), where r = 1, 2, 3, .... , 10$
1.  2051
2.  2049
3.  2076
4.  1052

$Find the sum of the series \frac{27}{8} + \frac{9}{4} + \frac{3}{2} + ... \infty .$
1.  $\frac{81}{8}$
2.  $\frac{27}{8}$
3.  $\frac{81}{16}$
4.  $\frac{9}{8}$

if the second and the seventh terms of a Harmonic Progression are  $\frac{1}{5} \mathrm{and} \frac{1}{25}$ then find the series. 
1. $1, \frac{1}{5}, \frac{1}{9}, ...$
2. $\frac{1}{2}, \frac{1}{5}, \frac{1}{8}, ...$
3. $\frac{1}{7}, \frac{1}{5}, \frac{1}{3}, ...$
4.   $\frac{1}{3}, \frac{1}{5}, \frac{1}{7}, ....$

$\mathrm{The} 10\mathrm{th} \mathrm{term} \mathrm{of} \mathrm{Harmonic} \mathrm{Progression} \frac{1}{5}, \frac{4}{19}, \frac{2}{9}, \frac{4}{17}, ... \mathrm{is} \mathrm{\_\_\_\_\_\_\_} .$
1.  $\frac{11}{4}$
2.  $\frac{13}{4}$
3.  $\frac{4}{13}$
4.  $\frac{4}{11}$

If the ratio of the arithmetic mean and the geometric mean of two positive number 3 : 2, then find the ratio of the geometric mean and harmonic mean of the numbers.
1. 2 : 3
2. 9 : 4
3. 3 : 2 
4. 4 : 9

If A, G, and H are AM, GM and HM of any two given numbers, then find the relation between A, G and H.
1.  $A^2 = GH$
2.  $G^{2 } = AH$
3.  $H^2 = AG$
4.  $G^3 = A^{2}H$

Find the least value of n for which the sum 1 + 2 + $2^2$ + ... to n term is greater than 3000.
1.  8
2.  10
3.  12
4.  15

Find the HM of $\frac{1}{7} \mathrm{and} \frac{1}{12}.$
1.   $\frac{1}{19}$
2.  $\frac{2}{19}$
3.  $\frac{3}{19}$
4.  $\frac{4}{19}$
 

$\mathrm{In} \mathrm{a} \mathrm{series}, \mathrm{if} {\mathrm{t}}_{\mathrm{n}} = \frac{{\mathrm{n}}^2 - 1}{\mathrm{n} + 1}, \mathrm{then} {\mathrm{S}}_6 - {\mathrm{S}}_3 = \mathrm{\_\_\_\_\_\_\_\_\_\_} .$
1.  3
2.  10
3.  24
4.  36

Number of rectangles are in the following figure are ____________ .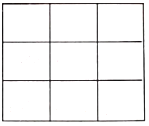

1.  9
2.  10
3.  24
4.  36

Find the number of the term to be added in the series 27, 9, 3, ... so that the sum is $\frac{1093}{27}$ .
1.  6
2.  7
3.  8
4.  9

Find the value of $\mathrm{p} \left(\mathrm{p} > 0\right) \mathrm{if} \frac{15}{4} + \mathrm{p}, \frac{5}{2} + 2\mathrm{p} \mathrm{and} 2 + \mathrm{p}$ are the three consecutive term of geometric progression.
1.  $\frac{3}{4}$
2.  $\frac{1}{4}$
3.  $\frac{5}{3}$
4.  $\frac{1}{2}$

Five distinct positive integers are in arithmetic progression with a positive common difference. If their sum is 10020, then find the smallest possible value of the last term.
1.  2002
2.  2004
3.  2006
4.  2008

in a triangle, the length of the sides are in arithmetic progression. If the length of the sides of the triangle are integers, which of the following could be the length of the shortest side?
1.  2125
2.  1700
3.  1275
4.  1150

$\mathrm{If} {\mathrm{S}}_1 = 3, 7, 11, 15, ... \mathrm{upto} 125 \mathrm{terms} \mathrm{and} {\mathrm{S}}_2 = 4, 7, 10, 13, 16, ... \mathrm{upto} 125 \mathrm{terms} \mathrm{are} \mathrm{in} {\mathrm{S}}_1 \mathrm{that} \mathrm{are} \mathrm{there} \mathrm{in} {\mathrm{S}}_{2 }?$
1.  29
2.  30
3.  31
4.  32

The first term and the mth term of a geometric progression are a and n respectively and its nth term is m. Then its (m + 1 - n)th term is __________. 
1.  $\frac{ma}{n}$ 
2.  $\frac{na}{m}$
3.  $mna$
4.  $\frac{mn}{a}$

the sum of the terms of an infinite geometric progression is 3 and the sum of the squares of the term is 81. Find the first term of the series.
1.  5
2. $\frac{27}{5}$  
3.  $\frac{31}{6}$
4.  $\frac{19}{3}$

$\mathrm{If} {\log }_{\sqrt{2}} \mathrm{x} + {\log }_{\sqrt{\sqrt{2}}} \mathrm{x} + {\log }_{\sqrt{\sqrt{\sqrt{2}}}} \mathrm{x} + ... \mathrm{upto} 7 \mathrm{terms} = 1016, \mathrm{find} \mathrm{the} \mathrm{value} \mathrm{of} \mathrm{x}.$
1.  4
2.  16
3.  64
4. 2

For which of the following values of $\mathrm{x} \mathrm{is} 8^{1 + \mathrm{sinx} +{\sin }^2\mathrm{x} +{\sin }^3\mathrm{x} + ...+\infty } = 64 ?$
1.  $60°$
2.  $135°$
3.  $45°$
4.  $30°$

Find the sum of all the multiples of 6 between 200 and 1100.
1.  96750
2.  95760
3.  97560
4.  97650

$If the kth term of a HP is \lambda p and the \lambda th term is kp and k \ne \lambda , then the pth term is \_\_\_\_\_\_\_\_\_\_\_.$
1.  $k^2\lambda$
2.  $k^{2}p$
3.  $p^{2}k$
4.  $\lambda k$

If six harmonic means are inserted between 3 and $\frac{6}{23}$, then the fourth harmonic mean is 
1.  $\frac{6}{11}$
2.  $\frac{6}{17}$
3.  $\frac{3}{7}$
4.   $\frac{3}{10}$

If a, b and c are positive numbers in arithmetic progression. and ${\mathrm{a}}^2, {\mathrm{b}}^2 \mathrm{and} {\mathrm{c}}^2$ are in geometric progression, then ${\mathrm{a}}^3, {\mathrm{b}}^{3 } \mathrm{and} {\mathrm{c}}^3 \mathrm{are} \mathrm{in}$
(A)  Arithmetic Progression 
(B)  Geometric Progression 
(C)  Harmonic Progression 
1.  (A) and (B) only
2.  only (C)
3.  (A), (B) and (C)
4.  only (B)

The arithmetic mean A of two positive numbers is 8. The harmonic mean H and the geometric mean G of the numbers satisfy the relation 4H + $G^2 = 90.$ Then one of the two numbers is _______.
1.  6
2.  8
3.  12
4.  14

$\mathrm{The} \mathrm{infinite} \mathrm{sum} \sum _{\mathrm{n} = 1}^{\infty }\left(\frac{5^{\mathrm{n}} + 3^{\mathrm{n}}}{5^{\mathrm{n}}}\right) \mathrm{is} \mathrm{equal} \mathrm{to}$
1.  $\frac{3}{2}$ 
2.  $\frac{3}{5}$
3.  $\frac{2}{3}$
4.  none of these

$$\begin{gathered} \mathrm{If} \mathrm{x} = 3 + \frac{3}{\mathrm{y}} + \frac{3}{{\mathrm{y}}^2} + \frac{3}{{\mathrm{y}}^3} + ... +\infty , \mathrm{then} \mathrm{show} \mathrm{that} \mathrm{y} = \frac{\mathrm{x}}{\mathrm{x} - 3}. (\mathrm{Where} \left|\mathrm{y}\right| < 1). \mathrm{The} \mathrm{following} \mathrm{are} \mathrm{the} \mathrm{steps} \mathrm{involved} \mathrm{in} \mathrm{saving} \mathrm{the} \mathrm{above} \mathrm{problem}. \mathrm{Arrange} \mathrm{them} \mathrm{in} \mathrm{sequential} \mathrm{order}. \\ \left(\mathrm{A}\right) \mathrm{xy} - 3\mathrm{y} = \mathrm{x} \\ \left(\mathrm{B}\right) \mathrm{x} = 3\left(\frac{1}{1 - {\displaystyle \frac{1}{\mathrm{y}}}}\right) \\ \left(\mathrm{C}\right) \mathrm{y}(\mathrm{x} - 3) = \mathrm{x} \\ (\mathrm{D} ) \mathrm{x} = 3 \left(\frac{\mathrm{y}}{\mathrm{y} - 1}\right) \end{gathered}$$
1.  BDCA
2.  BDAC
3.  CABD
4.  ACBD

Find the harmonic mean of 5 and 3.
The following are the steps involved in solving the above problem. Arrange them in sequential order.
$$\begin{gathered} \left(A\right) HM = \frac{2 x 5 x 3}{5 + 3} \\ \left(B\right) We know that the harmonic mean of a, b is \frac{2ab}{a + b}. \\ \left(C\right) Here, a = 5 and b = 3 \\ \left(D\right) HM = \frac{30}{8} = \frac{15}{4} \end{gathered}$$
1.  BCDA
2.  BCAD
3.  ABCD
4.  BADC

$$\begin{gathered} The numbers h_1, h_2, h_3, h_4, ... , h_{10} are in harmonic progression and a_1, a_2, ... , a_{10} are in arithmetic progression. If a_1 = h_1 = 3 \\ and a_7 = h_7 = 39, then the value of a_4 x h_4 is \_\_\_\_\_\_\_\_\_\_ . \end{gathered}$$
1.  $\frac{13}{49}$
2.  $\frac{182}{3}$
3.  $\frac{7}{13}$
4.  117

Find the value of 
$\left(1 + \frac{1}{2}\right) \left(1 + \frac{1}{4}\right) \left(1 + \frac{1}{16}\right) \left(1 + \frac{1}{256}\right) ... \infty$
1.  1
2.  2
3.  $\frac{1}{3}$
4.  $\frac{1}{4}$

The rato of the sum of n terms of two arithmetic progressions is given by (2n + 3) : (5n - 7). Find the ratio of their nth terms.
1.  (4n + 5) : (10n + 2)
2.  (4n + 1) : (10n - 12)
3.  (4n - 1) : (10n + 8)
4.  (4n - 5) : (1on - 2)

$If x = \frac{1}{\sqrt{2}} + \frac{1}{2} + \frac{1}{2\sqrt{2}} + ... + \infty , then find the value of x + \frac{1}{x}.$
1.  $\sqrt{2}$
2.  $2\sqrt{2}$
3.  $3\sqrt{2}$
4.  $4\sqrt{3}$

In a GP of 6 terms, the first and the last terms are $\frac{{\mathrm{x}}^3}{{\mathrm{y}}^2} \mathrm{and} \frac{{\mathrm{y}}^3}{{\mathrm{x}}^2}$ respectively. Find the ratio of 3rd and 4th terms of that GP.
1.  $x^{2 }: y$
2.  $y^2 : x$
3.  $y : x$
4.  $x : y$

$$\begin{gathered} If x = 3 + \frac{3}{y} + \frac{3}{y^2} + \frac{3}{y^y} + ... + \infty , the y = \_\_\_\_\_\_\_\_\_ . \\ (where \left|y\right| > 1) . \end{gathered}$$
1.  $\frac{x}{3}$
2.  $\frac{x}{x - 3}$
3.  $\frac{1 - x}{3}$
4.  $1 - \frac{3}{x}$

$\mathrm{Find} \mathrm{the} \mathrm{sum} \mathrm{of} \frac{0.3}{0.5} + \frac{0.33}{0.55} + \frac{0.333}{0.555} + ... \mathrm{to} 15 \mathrm{terms}.$
1.  10
2.  9
3.  3
4.  5

In a Gp, if the fourth term is square of the second term, then the relation between the first and common ratio is _________.
1. $a = r$  
2.  $a = 2r$
3.  $2a = r$
4.  $r^{2 } = a$

For which of the following values of x is $\left(0°<\mathrm{x}<90°\right) {61}^{1 + \mathrm{cosx} + {\cos }^3 \mathrm{x}+ {\cos }^3\mathrm{x} + ... \infty } = 256 ?$
1.  $30°$
2.  $45°$
3.  $60°$
4.  $15°$

$\mathrm{If} {\mathrm{t}}_{2 } \mathrm{and} {\mathrm{t}}_3 \mathrm{of} \mathrm{a} \mathrm{GP} \mathrm{are} \mathrm{p} \mathrm{and} \mathrm{q}, \mathrm{respectively}, \mathrm{them} {\mathrm{t}}_5 = \mathrm{\_\_\_\_\_\_\_\_\_} .$
1.  $\mathrm{p}{\left(\frac{\mathrm{q}}{\mathrm{p}}\right)}^3$
2.  $\mathrm{p}{\left(\frac{\mathrm{q}}{\mathrm{p}}\right)}^2$
3.  $\frac{{\mathrm{p}}^2}{{\mathrm{q}}^3}$
4.  ${\mathrm{p}}^2{\mathrm{q}}^2$

If a, b, c, d are in GP, then ${(\mathrm{a} + \mathrm{b})}^2$ = __________ .
1.  (b+ d)(a + d)
2.  (a + d)(c +d)
3.  (a + b)(c +d)
4.  (a + c)(b + d)

a, b, c are in GP. If a is the first term and c is the common ratio, then b = ________ .
1.  1
2.  $\frac{1}{a}$
3.  $\frac{1}{c}$
4.  None of these

$\mathrm{In} \mathrm{a} \mathrm{GP} \mathrm{of} 7 \mathrm{terms}, \mathrm{the} \mathrm{last} \mathrm{term} \mathrm{is} \frac{64}{81} \mathrm{and} \mathrm{the} \mathrm{common} \mathrm{ratio} \mathrm{is} \frac{2}{3}. \mathrm{Find} \mathrm{the} 3\mathrm{rd} \mathrm{term}.$
1.  4
2.  9
3.  8
4.  12

An AP starts with a positive fraction and every alternate term is an integer. If the sum of the first 11 terms is 33, then the fourth term.
1.  2
2.  3
3.  5
4.  6

If the sum of 16 terms of an AP is 1624 and the first term is 500 times the common difference, then find the common difference.
1.  5
2.  $\frac{1}{2}$
3.  $\frac{1}{5}$
4.  2

Find the sum of the series 1 + (1 + 2) + (1 + 2 + 3) + ( + 2 + 3 + 4) + ... + (1 + 2 + 3 + ... + 20).
1.  1470
2.  1540
3.  1610
4.  1370

$$\begin{gathered} \mathrm{Evaluate} \underset{}{\overset{}{\sum 2\mathrm{i}, \mathrm{where} \mathrm{i} = 2, 3, 4, ..., 10.}} \\ 1. 2044 \\ 2. 2048 \\ 3. 1024 \\ 4. 1022 \end{gathered}$$