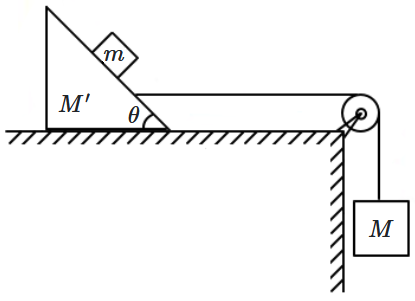
The value of \(M\) of the hanging block is in the figure, which will prevent the smaller block (\(m\)\(=\)\(1\) kg) from slipping over the triangular block. All the surfaces are smooth and string and pulley are ideal. (Given: \(M'\)\(=4\) kg and \(\theta\) \(=37^\circ\))

           
1. \(12\) kg
2. \(15\) kg
3. \(10\) kg
4. \(4\) kg

A plumb line is suspended from a ceiling of a car moving with horizontal acceleration of a. What will be the angle of inclination with vertical 

1. tan^–1(a/g)

2. tan^–1(g/a)

3. cos^–1(a/g)

4. cos^–1(g/a)

A block is kept on a frictionless inclined surface with an angle of inclination 'α'. The incline is given an acceleration 'a' to keep the block stationary. Then a is equal to 

(1) g

(2) gtanα

(3) g/tanα

(4) gcosecα

On the horizontal surface of a truck (μ = 0.6), a block of mass 1 kg is placed. If the truck is accelerating at the rate of 5m/sec² then frictional force on the block will be 

(1) 5 N

(2) 6 N

(3) 5.88 N

(4) 8 N

A block of mass m is in contact with the cart C as shown in the figure.

The coefficient of static friction between the block and the cart is $\mu .$The acceleration $\alpha$ of the cart that will prevent the block from falling satisfies

1. $\alpha >\frac{mg}{\mu }$                                       2. $\alpha >\frac{g}{\mu m}$

3. $\alpha \ge \frac{g}{\mu }$                                          4. $\alpha <\frac{g}{\mu }$