My Notes
A spring \(40~\text {mm}\) long is stretched by the application of a force. If \(10 ~\text{N}\) force required to stretch the spring through \(1 ~\text{mm,}\) then work done in stretching the spring through \(40 ~\text{mm}\) is
1. \(84~\text{J}\)
2. \(68~\text{J}\)
3. \(23~\text{J}\)
4. \(8~\text{J}\)
Two springs with spring constants = 1500 N/m and = 3000 N/m are stretched by the same force. The ratio of potential energy stored in the springs will be
1. 2:1
2. 1:2
3. 4:1
4. 1:4
A block of mass 2 kg moving with velocity of 10 m/s on a smooth surface hits a spring of force constant N/m as shown. The maximum compression in the spring is

1. 5 cm
2. 10 cm
3. 15 cm
4. 20 cm
A block of mass m = 25 kg on a smooth horizontal surface with a velocity =3 meets the spring of spring constant k = 100 N/m fixed at one end as shown in the figure. The maximum compression of the spring and velocity of the block as it returns to the original position respectively are:

1. 1.5 m, -3
2. 1.5 m, 0
3. 1.0 m, 3
4. 0.5 m, 2
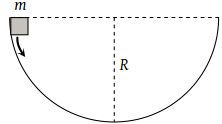
A mass m slips along the wall of a semispherical surface of radius R. The velocity at the bottom of the surface is [ MP PMT 1993]
1.
2.
3.
4.
