My Notes
Two small spheres each carrying a charge q are placed r meter apart. If one of the spheres is taken around the other one in a circular path of radius r, the work done will be equal to
1. Force between them × r
2. Force between them × 2πr
3. Force between them / 2πr
4. Zero
If a unit positive charge is taken from one point to another over an equipotential surface, then -
1. Work is done on the charge
2. Work is done by the charge
3. Work done is constant
4. No work is done
In the electric field of a point charge q, a certain charge is carried from point A to B, C, D and E. Then the work done
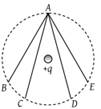
1. Is least along the path AB
2. Is least along the path AD
3. Is zero along all the paths AB, AC, AD and AE
4. Is least along AE
On rotating a point charge having a charge \(q\) around a charge \(Q\) in a circle of radius \(r,\) the work done will be:
| 1. | \(q \times2 \pi r\) | 2. | \(q \times2 \pi Q \over r\) |
| 3. | zero | 4. | \(Q \over 2\varepsilon_0r\) |
| 1. | The electric potential at the surface of the cube is zero. |
| 2. | The electric potential within the cube is zero. |
| 3. | The electric field is normal to the surface of the cube. |
| 4. | The electric field varies within the cube. |
© 2024 GoodEd Technologies Pvt. Ltd.