A wheel comprises of a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is
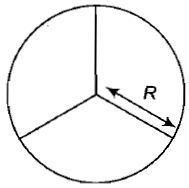

1. \(\left(M + \frac{m}{4}\right) R^{2} \)
2. \(\left(M + m\right) R^{2} \)
3. \(\left(M + 3 m\right) R^{2} \)
4. \(\left(\frac{M + m}{2}\right) R^{2}\)


The angular velocity of a body changes from rev./sec to 1 rev./sec. without applying any torque. The ratio of its radius of gyration in two situations is :
1. 5: 1
2. 1: 5
3. 1: 25
4. 25: 1
A solid cylinder and a solid sphere, both having the same mass and radius, are released from a rough inclined plane. Both roll without slipping. Then,
1. the force of friction that acts on the two is the same
2. the force of friction is greater in the case of a sphere than in a cylinder
3. the force of friction is greater in the case of a cylinder than in a sphere
4. the force of friction will depend on the nature of the surface of the body that is moving and that of the inclined surface and is independent of the shape and size of the moving body
A homogeneous disc of mass 2 kg and radius 15 cm is rotating about its axis (which is fixed) with an angular velocity of 4 rad/sec. The linear momentum Of the disc is
1. 1.2 kg m/sec
2. 1.0 kg m/sec
3. 0.6 kg m/sec
4. None of these
A rigid body rotates about a fixed axis with a variable angular velocity equal to \(\alpha -\beta t\), at the time \(t\), where \(\alpha , \beta\) are constants. The angle through which it rotates before it stops is:
| 1. | \(\frac{\alpha^{2}}{2 \beta}\) | 2. | \(\frac{\alpha^{2} -\beta^{2}}{2 \alpha}\) |
| 3. | \(\frac{\alpha^{2} - \beta^{2}}{2 \beta}\) | 4. | \(\frac{\left(\alpha-\beta\right) \alpha}{2}\) |
For the uniform T shaped structure, with mass \(3~ \text M\), the moment of inertia about an axis normal to the plane and passing through O would be
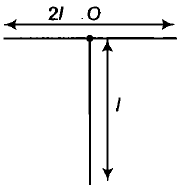

1. \({ 2 \over 3} \text {MI}^2\)
2. \(\text {MI}^2\)
3. \({ MI^2 \over 3}\)
4. None of these
1. \(\frac{5}{2}I\)
2. \(3I\)
3. \(\frac{3}{2}I\)
4. \(4I\)
A rigid body rotates with an angular momentum L. If its rotational kinetic energy is made 4 times, its angular momentum will become
1. 4L
2. 16L
3.
4. 2L
Four particles of mass \(m_1 = 2m\), \(m_2=4m\), \(m_3 =m \), and \(m_4\) are placed at the four corners of a square. What should be the value of \(m_4\) so that the centre of mass of all the four particles is exactly at the centre of the square?

| 1. | \(2m\) | 2. | \(8m\) |
| 3. | \(6m\) | 4. | None of these |
Angular momentum of a body is defined as the product of
1. Mass and angular velocity
2. Centripetal force and radius
3. Linear velocity and angular velocity
4. Moment of inertia and angular velocity


