Volume, pressure, and temperature of an ideal gas are \(V,\) \(P,\) and \(T\) respectively. If the mass of its molecule is \(m\), then its density is: [\(k\)=Boltzmann's constant]

1.	\(mkT\)	2.	\(P \over kT\)
3.	\(P \over kTV\)	4.	\(Pm \over kT\)

One liter of gas A and two liters of gas B, both having the same temperature 100$°$C and the same pressure 2.5 bar will have the ratio of average kinetic energies of their molecules as:

1. 1:1       

2. 1:2     

3. 1:4       

4. 4:1

On \(0^{\circ}\text{C}\), the pressure measured by the barometer is \(760\) mm.  What will be pressure at \(100^{\circ}\text{C}\)?
1. \(760~\text{mm}\)
2. \(730~\text{mm}\)
3. \(780~\text{mm}\)
4. None of these

By what percentage, should the pressure of a given mass of gas be increased, so as to decrease its volume by 10% at a constant temperature?

1. 5%     

2. 7.2 %       

3. 12.5%         

4. 11.1%

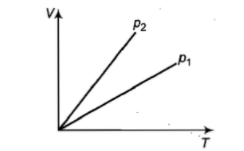
In the adjacent V-T diagram what is the relation between $P_{1 }and P_2$ ?

1. $P_2=P_1$                               

2. $P_2>P_1$

3. $P_2<P_1$                                 

4. cannot be predicated
 

Which one of the following graph is correct at constant pressure?

1.		2.
3.		4.

The root-mean-square velocity of the molecules in a sample of helium is $\frac{5}{7}th$ of that of the molecules in a sample of hydrogen.  If the temperature of the hydrogen gas is 0$°$C, that of the helium sample is about:

1. 0$°$C       

2. 5.6$°$C      

3. 273$°$C         

4. 100$°$C

The kinetic energy of one gram molecule of a gas at standard temperature and pressure is: (R = 8.31 J/mol-K)

1. 0.56 $\times {10}^4 J$             

2. $1.3\times {10}^2 J$

3. $2.7\times {10}^2 J$                 

4. $3.4\times {10}^3 J$

Gases exert pressure on the walls of containing vessel because  the gas molecules:

1. Possess momentum

2. collide with each other

3. have finite volume

4. obey gas laws

The equation of state for 5 g of oxygen at a pressure P and temperature T, when occupying a volume V, will be: (where R is the constant)

1. PV = 5RT

2. PV = $\left(\frac{5}{2}\right)RT$

3. PV = $\left(\frac{5}{16}\right)RT$

4. PV = $\left(\frac{5}{32}\right)RT$