Two convex lenses of focal lengths $f_1 and f_2$ are separated co-axially by a distance d. The power of the combination will be zero if d equals to

1. $\sqrt{f_1{f}_2}$

2. $f_1+f_2$

3. $\frac{f_1-f_2}{2}$

4. $\frac{f_1+f_2}{2}$

A thin equiconvex lens of power P is cut into three parts A, B, and C as shown in the figure. If $P_1, P_2 \mathrm{and} P_3$ are powers of the three parts respectively, then 

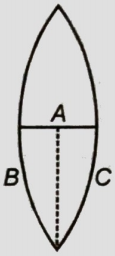
1.  $P_1 = P_2 = P_3$

2.  $P_1 > P_2 = P_3$

3.  $P_1 < P_2 = P_3$

4.  $P_2 = P_3 = 2P_1$

A light beam containing red, yellow and blue color, falls on the interface of glass-air as

shown. If the yellow light is just totally internally reflected then emergent ray in air contain

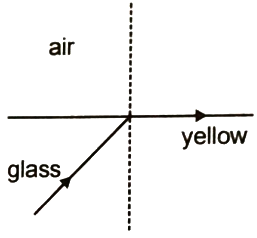
1.  Both red and blue color

2.  Only red color

3.  Only blue color

4.  No color

An astronomical telescope has angular magnification of \(40\) in its normal adjustment. If focal length of eyepiece is \(5\) cm, the length of the telescope is:
1. \(190\) cm
2. \(200\) cm
3. \(205\) cm
4. \(210\) cm

A convex lens forms the image of an object of the same magnification when the object is placed at 10 cm and 20 cm from the lens. The focal length of the lens is:

(1) 5 cm

(2) 15 cm

(3) 25 cm

(4) 30 cm

A, B, and C are three optical media of respective critical angles ${\mathrm{i}}_{\mathrm{A}}, {\mathrm{i}}_{\mathrm{B}} \mathrm{and} {\mathrm{i}}_{\mathrm{C}}$. Total internal reflection of light can occur from A to B and also from B to C but not from C to A, then the correct relation between critical angles is 

1. $i_A<i_B<i_C$

2. $i_A>i_B>i_C$

3. $i_A=i_B=i_C$

4. $i_C>i_A>i_B$

When a telescope is focussed for parallel rays then its magnifying power is 10 and the distance between the objective and the eyepiece is 22 cm. The focal length of each lens is

1.  20 cm, 2 cm

2.  11 cm, 9 cm

3.  10 cm, 5 cm

4.  18 cm, 2 cm

An object O is placed on one side of two glass slabs A and B of thickness 1.5 cm and refractive index 1.5. The position of the image of O, when viewed from the other side of slab B, will be:

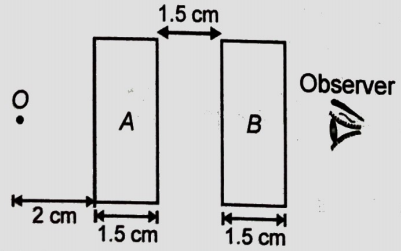
1.  1 cm away from slab A

2.  1.5 cm away from slab A

3.  2 cm away from slab A

4.  2.5 cm away from slab A

The focal length of an equiconvex glass lens(${\mu }_{glass}= 1.5$) in air is 20 cm. The relative refractive index of  glass with respect to water is $\frac{9}{8}$. If the lens is dipped in water, then its new focal length in water is-

1.  20 cm

2.  -20 cm

3.  80 cm

4.  -80 cm

A virtual image of an object is formed by a concave lens. The lens is then coupled (kept in contact) with a convex lens. A virtual image is again formed. Then the image, now

1. Shifts away from lens system

2. Shifts towards lens system

3. Remains at its original position

4. Data are insufficient to predict whether it will shift towards or away from the lens system.