A homogeneous solid cylinder of length L(L<H/2) . Cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the fig. The lower density liquid is open to atmosphere having pressure . Then density D of solid is given by

1.
2.
3.
4.

A block of ice floats on a liquid of density 1.2 in a beaker. The level of liquid when ice completely melts-
1. Remains same
2. Rises
3. Lowers
4. (1), (2) or (3)
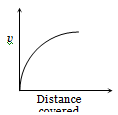
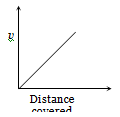
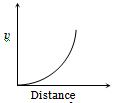
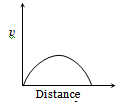
A lead shot of 1mm diameter falls through a long column of glycerine. The variation of its velocity v with distance covered is represented by
1. 
2. 
3. 
4. 
The surface tension of liquid is 0.5 N/m. If a film is held on a ring of area 0.02 , its surface energy is
1.
2.
3.
4.
A film of water is formed between two straight parallel wires of length 10cm each separated by 0.5 cm. If their separation is increased by 1 mm while still maintaining their parallelism, how much work will have to be done (Surface tension of water =)
1.
2.
3.
4.
A drop of mercury of radius 2 mm is split into 8 identical droplets. Find the increase in surface energy. (Surface tension of mercury is )
1.
2.
3.
4.
Two small drops of mercury, each of radius r, coalesce to form a single large drop. The ratio of the total surface energies before and after the change is
1. 2.
3. 2:1 4. 1:2
When a large bubble rises from the bottom of a lake to the surface, its radius doubles. If atmospheric pressure is equal to that of column of water height H, then the depth of lake is
1. H
2. 2H
3. 7H
4. 8H
If pressure at half the depth of a lake is equal to 2/3rd the pressure at the bottom of the lake, then the depth of the lake is:
| 1. | 10 m | 2. | 20 m |
| 3. | 60 m | 4. | 30 m |
A spherical drop of water has a radius of 1 mm. If the surface tension of water is N/m, the difference in pressures inside and outside the spherical drop is:
| 1. | 35 N / m2 | 2. | 70 N / m2 |
| 3. | 140 N / m2 | 4. | Zero |






