A uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in horizontal position. Given that the moment of inerita of the rod about A is $\frac{{\mathrm{ml}}^2}{3}$ the initial angular acceleration of the rod will be

 

$1. \frac{2\mathrm{g}}{3\mathrm{l}}$
$2. \mathrm{mg}\frac{\mathrm{l}}{2}$
$3. \frac{3}{2}\mathrm{gl}$
$4. \frac{3\mathrm{g}}{2\mathrm{l}}$

                
1. \(\frac{PQ+PR+QR}{3}\)
2. \(\frac{PQ+PR}{3}\)
3. \(\frac{PQ+QR}{3}\)
4. \(\frac{PR+QR}{3}\)

Two particles of equal mass have coordinates (2m,4m,6m) and (6m,2m,8m). Of these one particle has velocity ${\mathrm{v}}_1=\left(2\hat{\mathrm{i}}\right)$ m/s and another particle has velocity ${\mathrm{v}}_2=\left(2\hat{j}\right)$ m/s at time t = 0. The coordinate of their centre of mass at time t = 1 s will be

1. (4m,4m,7m)

2. (5m,4m,7m)

3. (2m,4m,6m)

4. (4m,5m,4m)

The M.I. of a body about the given axis is 1.2 kg x ${\mathrm{m}}^2$ initially the body at rest. In order to the rotational kinetic energy of 1500 J, the angular acceleration of 25 rad/${\sec }^2$ must be about that axis for the duration of

1.  4 sec

2.  2 sec

3.  8 sec

4.  10 sec

A loop rolls down on the inclined plane. The fraction of its total kinetic energy that is associated with rotational motion is

1.  1: 2

2.  1: 3

3.  1: 4

4.  2: 3

A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass

1. of the box remains constant 

2. of the box plus the ball system remains constant

3. of the ball remains constant

4. of the ball relative to the box remains constant

A solid sphere is rolling on a frictionless surface, as shown in the figure with a translational velocity of v m/s. If a sphere climbs up to a height h, then the value of v would be:
                 

1. $\ge \sqrt{\frac{10}{7}\mathrm{gh}}$                                                   

2. $\ge \sqrt{2\mathrm{gh}}$

3. $2\mathrm{gh}$                                                             

4. $\frac{10}{7}\mathrm{gh}$

The disc is placed on a rough horizontal surface and given only angular velocity ${\omega }_0$. The velocity of the centre of mass when it starts rolling is:

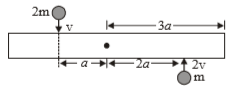
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two-point
masses m and 2m moving in the same horizontal plane with speeds 2v and v
respectively strike the bar as shown below in the figure and stick to the bar after the collision. Denoting angular velocity about the center of mass, total energy, and center of mass velocity of $\omega$, E and ${\mathrm{v}}_{\mathrm{c}}$ respectively, we have after collision

1.  ${\mathrm{v}}_{\mathrm{c}} = 2 \mathrm{m}/\mathrm{s}$

2.  $\mathrm{\omega } = \frac{3}{5}\frac{\mathrm{v}}{\mathrm{a}}$

3.  $\mathrm{\omega } = \frac{\mathrm{v}}{5\mathrm{a}}$

4.  $\mathrm{E} = \frac{2}{3} {\mathrm{mv}}^2$

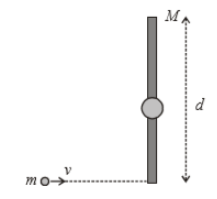
A particle of mass m is moving at speed v perpendicular to a rod of length d and mass M = 6m which pivots around a frictionless axle running through its centre. It strikes and sticks to the end of the rod. The moment of inertia of the rod about its centre is $M{d}^2/12$. Then the angular speed  of the system just after the collision is:

1. 2v/3d

2. 2v/d

3. v/d

4. v