Two springs with spring constants k1k1 = 1500 N/m and k2k2 = 3000 N/m are stretched by the same force. The ratio of potential energy stored in the springs will be
1. 2:1
2. 1:2
3. 4:1
4. 1:4
A block of mass 2 kg2 kg moving with a velocity of 10 m/s10 m/s on a smooth surface hits a spring of force constant 80×103 N/m80×103 N/m as shown in the figure. The maximum compression in the spring will be:

1. 5 cm5 cm
2. 10 cm
3. 15 cm
4. 20 cm
A particle of mass 10 kg is moving with velocity of 10√x m/s, where x is displacement . The work done by net force during the displacement of particle form x = 4 to x = 9 m is
1. 1250 J
2. 1000 J
3. 3500 J
4. 2500 J
The relation between velocity (v) and time (t) is vα√t, then which one of the following quantity is constant:
1. Force
2. Power
3. Momentum
4. Kinetic Energy
A particle is moving on the circular path of the radius (R) with centripetal acceleration ac=k2Rt2. Then the correct relation showing power (P) delivered by net force versus time (t) is
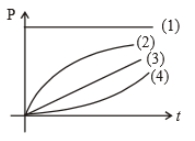
1. 1
2. 2
3. 3
4. 4
1. 43 J
2. 56 J
3. 32 J
4. 75 J
A force F is applied on a body which moves with a velocity v in the direction of the force, then the power will be
1. Fv2
2. Fv
3. F/v2
4. F/v
A mass m slips along the wall of a semispherical surface of radius R. The velocity at the bottom of the surface is [ MP PMT 1993]
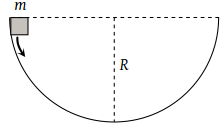
(1) √Rg
(2) √2Rg
(3) 2√πRg
(4) √πRg
Three different objects of masses m1, m2 and m3 are allowed to fall from rest and from the same point ‘O’ along three different frictionless paths. The speeds of the three objects, on reaching the ground, will be in the ratio of
(1) m1:m2:m3
(2) m1:2m2:3m3
(3) 1 : 1 : 1
(4) 1m1:1m2:1m3
A sphere of mass m is tied to end of a string of length l and rotated through the other end along a horizontal circular path with speed v. The work done by centripetal force in full horizontal circle is
(1) 0
(2) (mv2l) . 2πl
(3) mg . 2πl
(4) (mv2l) . (l)







