The coordinates of a moving particle at any time \(t\) are given by \(x=\alpha t^3\) and \(y=\beta t^3.\) The speed of the particle at time \(t\) is given by:
1. \(\sqrt{\alpha^2+\beta^2}~\)
2. \(3t\sqrt{\alpha^2+\beta^2}~\)
3. \(3t^2\sqrt{\alpha^2+\beta^2}~\)
4. \(t^2\sqrt{\alpha^2+\beta^2}~\)
1. \(\sqrt{\alpha^2+\beta^2}~\)
2. \(3t\sqrt{\alpha^2+\beta^2}~\)
3. \(3t^2\sqrt{\alpha^2+\beta^2}~\)
4. \(t^2\sqrt{\alpha^2+\beta^2}~\)
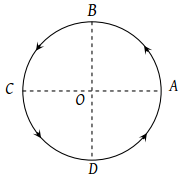
Figure shows a body of mass m moving with a uniform speed v along a circle of radius r. The change in velocity in going from A to B is
(1)
(2)
(3) v
(4) zero
The angle turned by a body undergoing circular motion depends on the time as given by the equation, \(\theta = \theta_{0} + \theta_{1} t + \theta_{2} t^{2}\). It can be deduced that the angular acceleration of the body is?
1. \(\theta_1\)
2. \(\theta_2\)
3. \(2\theta_1\)
4. \(2\theta_2\)
An aeroplane is flying at a constant horizontal velocity of 600 km/hr at an elevation of 6 km towards a point directly above the target on the earth's surface. At an appropriate time, the pilot releases a ball so that it strikes the target at the earth. The ball will appear to be falling
(1) On a parabolic path as seen by pilot in the plane
(2) Vertically along a straight path as seen by an observer on the ground near the target
(3) On a parabolic path as seen by an observer on the ground near the target
(4) On a zig-zag path as seen by pilot in the plane
A body is projected at such an angle that the horizontal range is three times the greatest height. The angle of projection is
(1)
(2)
(3)
(4)
Two bodies are projected with the same velocity. If one is projected at an angle of 30° and the other at an angle of 60° to the horizontal, the ratio of the maximum heights reached is
(1) 3 : 1
(2) 1 : 3
(3) 1 : 2
(4) 2 : 1
A cricketer can throw a ball to a maximum horizontal distance of 100 m. With the same effort, he throws the ball vertically upwards. The maximum height attained by the ball is
(1) 100 m
(2) 80 m
(3) 60 m
(4) 50 m
A particle is moving eastwards with velocity of \(5\) m/s. In \(10\) seconds the velocity changes to \(5\) m/s northwards. The average acceleration in this time is?
| 1. | zero |
| 2. | \(\frac{1}{\sqrt{2}}~ \text{m/s}^2\) toward north-west |
| 3. | \(\frac{1}{\sqrt{2}}~\text{m/s}^2\) toward north-east |
| 4. | \(\frac{1}{2}~\text{m/s}^2 \) toward north-west |
| 1. | \(0, ad\theta\) | 2. | \(a d\theta, 0\) |
| 3. | \(0,0\) | 4. | None of these |
A steam boat goes across a lake and comes back (a) On a quite day when the water is still and (b) On a rough day when there is uniform air current so as to help the journey onward and to impede the journey back. If the speed of the launch on both days was same, in which case it will complete the journey in lesser time
(1) Case (a)
(2) Case (b)
(3) Same in both
(4) Nothing can be predicted