Given that the current \(i_1=3A \sin \omega t\) and the current \(i_2=4A \cos \omega t,\) what will be the expression for the current \(i_3\)?

1. \(5 A \sin \left(\omega t+53^{\circ}\right) \)
2. \(5 A \sin \left(\omega t+37^{\circ}\right) \)
3. \(5 A \sin \left(\omega t+45^{\circ}\right) \)
4. \( 5 A \sin \left(\omega t+30^{\circ}\right)\)

1. \(5 A \sin \left(\omega t+53^{\circ}\right) \)
2. \(5 A \sin \left(\omega t+37^{\circ}\right) \)
3. \(5 A \sin \left(\omega t+45^{\circ}\right) \)
4. \( 5 A \sin \left(\omega t+30^{\circ}\right)\)
In a box \(Z\) of unknown elements (\(L\) or \(R\) or any other combination), an ac voltage \(E = E_0 \sin(\omega t + \phi)\) is applied and the current in the circuit is found to be \(I = I_0 \sin\left(\omega t + \phi +\frac{\pi}{4}\right)\). The unknown elements in the box could be:

| 1. | Only the capacitor |
| 2. | Inductor and resistor both |
| 3. | Either capacitor, resistor, and an inductor or only capacitor and resistor |
| 4. | Only the resistor |
The phase difference between emf and current through the choke coil maybe
1. 0
2. 85
3. 45
4. 30
1. \(\dfrac{\pi }{\sqrt{3}}~\text{H}\)
2. \(100~\text{H}\)
3. \(\dfrac{\sqrt{2}}{\pi }~\text{H}\)
4. \(\dfrac{\sqrt{3}}{\pi }~\text{H}\)
What is the phase difference between potential difference across the inductor and potential difference across the capacitor in a series LCR circuit?
1. Zero
What is the reading of the A.C voltmeter in the network as shown in the figure?
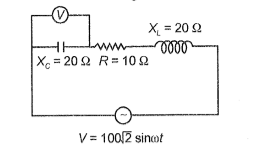
1. zero
2. 100 V
3. 200 V
4. 400 v
When an alternating voltage is given as; \(E = (6 \sin\omega t - 2 \cos \omega t)~\text V,\) what is its RMS value?
1. \(4 \sqrt 2 ~\text V\)
2. \(2 \sqrt 5 ~\text V\)
3. \(2 \sqrt 3 ~\text V\)
4. \(4 ~\text V\)
An LC circuit contains an inductor (L=25 mH) and a capacitor (C=25 mF) with an initial charge of Q0. At what time will the circuit have an equal amount of electrical and magnetic energy?
4. All of these
In which of the following circuits can the power factor be zero?
1. LC circuit
2. LCR circuit
3. Purely resistive circuit
4. Both (1) & (2)
In the given circuit, switch S is closed at t=0. After a long time, the iron rod is withdrawn from the inductor L. Then, the bulb
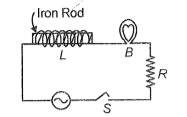
1. Glow with the same brightness
2. Glows more brightly
3. Gets dimmer
4. Stops glowing






