In Young's double-slit experiment, the distance between the slits is 1 mm. The wavelength of the light used is 600 nm. Fringe width of the interference pattern (as shown in the figure) is :
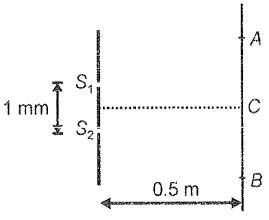
1. 0.6 mm
2. 0.3 mm
3. 0.4 mm
4. 0.2 mm

Four coherent sources of intensity \(I\) are superimposed constructively at a point. The intensity at that point is:
1. \(4I\)
2. \(8I\)
3. \(16I\)
4. \(24I\)
In Young's double-slit experiment, the intensities at the points of maxima and minima are and zero respectively. Intensities of individual sources are
1.
2.
3.
4.
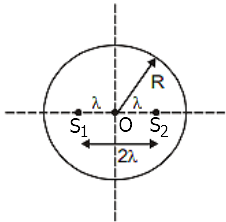
Two coherent light sources are kept at equal distances from the center of the circle on the same plane of the circle as shown in the figure. In one complete revolution on the circular path, the number of maxima observed is: (= wavelength of light used and 2λ<<R)
1. 4
2. 6
3. 8
4. 12
The ratio of intensities in consecutive maximas in a diffraction pattern due to a single slit is
1.
2.
3.
4. 1: 4: 9
In an interference pattern, the position of central maxima is \(5\) mm from a certain point \(P\) on the screen. The fringe width is \(0.6\) mm. The distance of the third minima from point \(P\) is:
1. \(3.2\) mm
2. \(3.3\) mm
3. \(3.5\) mm
4. \(3.8\) mm
In Young's double-slit experiment the separation between the slits is \(4\lambda\)\((\lambda\) is the wavelength of the light used). The maximum number of maxima formed on the screen placed at a distance of \(1~\text{m}\) from the slits is:
1. \(6\)
2. \(7\)
3. \(9\)
4. \(11\)
In Young's double-slit experiment, the separation between the slits is 0.5 mm. Source of light S is placed at a distance of 0.5 mm from the slit as shown in the figure. To have central maxima at mid-point O, the glass plate of refractive index 1.5 is placed in front of . The thickness of the plate is:
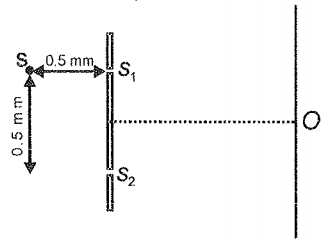
1. ( - 1) mm
2. ( + 1) mm
3. mm
4. mm
If the \(5\)th order maxima of wavelength \(4000~\mathring{A}\) in Young's double-slit experiment coincides with the \(n\)th order maxima of wavelength \(5000~\mathring{A},\) then \(n\) is equal to:
1. \(5\)
2. \(8\)
3. \(4\)
4. \(10\)
Light of wavelength 6000 in air enters a medium of refractive index 1.5. Frequency and wavelength of light in the medium respectively are
1.
2.
3.
4.