A sphere of mass M and radius R is falling in a viscous liquid. The terminal velocity attained by the sphere will be proportional to:

(1) ${\mathrm{R}}^2$

(2) R

(3) $\frac{1}{\mathrm{R}}$

(4) $\frac{1}{{\mathrm{R}}^2}$

Two water droplets merge with each other to form a larger droplet isothermally. In this process

(1) Energy is absorbed

(2) Energy is liberated

(3) Energy is neither liberated nor absorbed

(4) Some mass is converted into energy

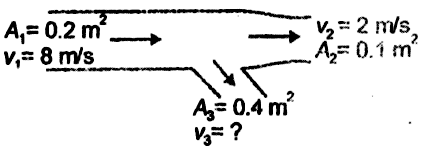
From the given diagram, what is the velocity \(v_3?\)
               
1. \(4~\text{m/s}\)
2. \(3~\text{m/s}\)
3. \(1~\text{m/s}\)
4. \(2~\text{m/s}\) 

The value of Reynold's number for which the flow of water through a pipe becomes turbulent is:

(1) 500

(2) 900

(3) 750

(4) 3000

The diameter of a syringe is \(4~\text{mm}\) and the diameter of its nozzle (opening) is \(1~\text{mm}\). The syringe is placed on the table horizontally at a height of \(1.25~\text{m}\). If the piston is moved at a speed of \(0.5~\text{m/s}\), then considering the liquid in the syringe to be ideal, the horizontal range of liquid is: \(\left(g = 10~\text{m/s}^2 \right)\)
1. \(4~\text{m}\)
2. \(8~\text{m}\)
3. \(0.4~\text{m}\)
4. \(0.2~\text{m}\)

A lead sphere of mass \(m\) falls in a viscous liquid with terminal velocity \(v\). Another lead sphere of mass \(M\) falls through the liquid with terminal velocity \(4v\). The ratio \(\frac{M}{m}\) is:
1. \(2\)
2. \(4\)
3. \(8\)
4. \(16\)

In the given figure, the velocity ${\mathrm{v}}_3$ of inc fluid flowing through the tube will be

(1) 3 m/s

(2) 4,5 m/s

(3) 3.5 m/s

(4) 5 m/s

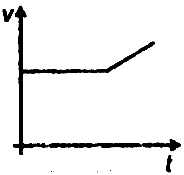
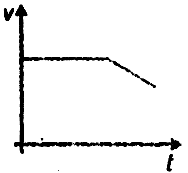
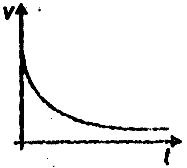
For amongst the following curves which one shows the variation of velocity with time for a small-sized spherical body falling vertically in a long column of viscous liquids

1.  

2.  

3.  

4.  

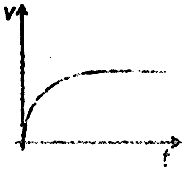
A sphere of mass m is dropped from a tall tower when it falls by 10 m, it attains terminal velocity and continues to fall at that speed. The work done by air friction against the sphere during the first 10 m is ${\mathrm{w}}_1$ and during next 10 m is ${\mathrm{w}}_2$ then

(1) ${\mathrm{w}}_1$ < ${\mathrm{w}}_2$

(2) ${\mathrm{w}}_1$ > ${\mathrm{w}}_2$

(3) ${\mathrm{w}}_1$ = ${\mathrm{w}}_2$

(4) ${\mathrm{w}}_1$ $\ge$ ${\mathrm{w}}_2$

Water is flowing from a source as shown in the figure. Let A be the cross-sectional area of the liquid flow at the time when velocity is 5 m/s. The cross-sectional area of the liquid flow when the water has descended by 10 meters is [Take g = 10 m/${\mathrm{s}}^2$]

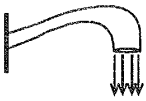
(1) 3A

(2) $\frac{\mathrm{A}}{3}$

(3) $\frac{\mathrm{A}}{2}$

(4) 2A