Work done by a force (F) in displacing a body by dx is given by W=∫F(x).dx. If the force is given as a function of displacement (x) by F(x)=(x2−2x+1)N, then work done by the force from x=0 to x=3 m is:
1. 3 J
2. 6 J
3. 9 J
4. 21 J
The impulse due to a force on a body is given by I=∫Fdt. If the force applied on a body is given as a function of time (t) as F=(3t2+2t+5)N, then impulse on the body between t=3 s to t=5 s is:
1. 175 kg-m/sec
2. 41 kg-m/sec
3. 216 kg-m/sec
4. 124 kg-m/sec
Which of the following option is not true, if →A = 3ˆi + 4ˆj and →B = 6ˆi + 8ˆj, where A and B are the magnitudes of →A and →B?
1. →A × →B = →0
2. AB = 12
3. →A·→B = 48
4. A=5
The angle made by the vector →A = √3ˆi + 3ˆj + 2ˆk with y-axis is:
1. sin-1(3√14)
2. sin-1(√74)
3. cos-1(43)
4. cos-1(35)
In the space, if the sum of vectors of unequal magnitude is zero, then the minimum number of vectors are:
1. 2
2. 3
3. 4
4. 5
If →A + →B is perpendicular to →A - →B , then which of the following statement is correct?
1. |→A| = |→B|
2. →A ⊥ →B
3. →A·→B = zero
4. (→A + →B)·(→A - →B) ≠ 0
The angle between the two vectors (−2ˆi+3ˆj+ˆk) and (ˆi+2ˆj−4ˆk) is:
1. 0∘
2. 90∘
3. 180∘
4. 45∘
If →a + →b + →c = →0; then which of the following statements is incorrect?
(1) →a, →b and →c must each be a null vector.
(2) The magnitude of →a+→b equals the magnitude of →c.
(3) The magnitude of ä can never be greater than the sum of the magnitudes of →b and →c
(4) ä must lie in the plane of →b and →c.
When a force of magnitude F acts on a body of mass m the acceleration produced in the body is a. If three coplanar forces of equal magnitude F act on the same body as shown in the figure, then acceleration produced is

1. 0
2. (√3 + 1)a
3. (√3 - 1)a
4. √3a
Three forces each of magnitude 1 N act along with the sides AB, BC, and CD of a regular hexagon. The magnitude of their resultant is:
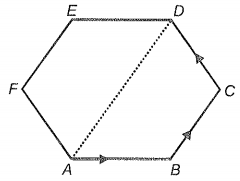
(1) 4N
(2) Zero
(3) 2 N
(4) 1 N






