If two force vectors $\overrightarrow{\mathrm{A}} \mathrm{and} \overrightarrow{\mathrm{B}}$ of the same magnitude are arranged in the following manner, the magnitude of resultant is maximum for?

                    

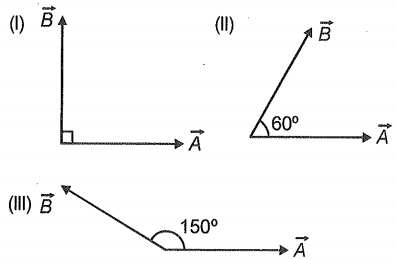
(1) (I)

(2) (II)

(3) Both (II) & (III)

(4) Both (I) & (II)

The minimum number of non-coplanar vectors whose vector sum can be zero is:

(1) 2

(2) 3

(3) 4

(4) 5

The resultant vector of $\overrightarrow{\mathrm{P}} \mathrm{and} \overrightarrow{\mathrm{Q}}$ makes angle ${\mathrm{\theta }}_1$ with $\overrightarrow{\mathrm{P}}$ and ${\mathrm{\theta }}_2$ with $\overrightarrow{\mathrm{Q}}$.Then-

1.  ${\mathrm{\theta }}_1 > {\mathrm{\theta }}_2$

2.  ${\mathrm{\theta }}_1 < {\mathrm{\theta }}_2 \mathrm{if} \mathrm{P} > \mathrm{Q}$

3.  ${\mathrm{\theta }}_1 < {\mathrm{\theta }}_2 \mathrm{if} \mathrm{P} < \mathrm{Q}$

4.  ${\mathrm{\theta }}_1 > {\mathrm{\theta }}_2 \mathrm{if} \mathrm{P} = \mathrm{Q}$

The figure shows ABCDEF as a regular hexagon. What is the value of $\overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{AC}} + \overrightarrow{\mathrm{AD}} + \overrightarrow{\mathrm{AE}} + \overrightarrow{\mathrm{AF}}$?

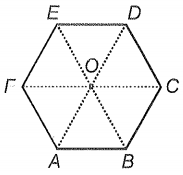
1.  $\overrightarrow{\mathrm{AO}}$

2.  $2\overrightarrow{\mathrm{AO}}$

3.  $4\overrightarrow{\mathrm{AO}}$

4.  $6\overrightarrow{\mathrm{AO}}$

A vector $\overrightarrow{\mathrm{A}}$, which has magnitude 8.0 is added to a vector $\overrightarrow{\mathrm{B}}$ which lies on the x-axis. The sum of these two vectors lies on the y-axis and has a magnitude twice the magnitude of $\overrightarrow{\mathrm{B}}$. The magnitude of the vector $\overrightarrow{\mathrm{B}}$

1.  8

2.  $\sqrt{2} \times 8$

3.  $\frac{8}{\sqrt{5}}$

4.  $8\sqrt{5}$

If $\overrightarrow{\mathrm{A}} = 2\hat{\mathrm{i}} + 3\hat{\mathrm{j}} + 6\hat{\mathrm{k}}$ and $\overrightarrow{\mathrm{B}} = 3\hat{\mathrm{i}} + 2\hat{\mathrm{j}} - \hat{\mathrm{k}}$, then the unit vector in the direction of $\overrightarrow{\mathrm{A}} + \overrightarrow{\mathrm{B}}$ is

1.  $\frac{\left(\hat{\mathrm{i}} - \hat{\mathrm{j}} - \hat{\mathrm{k}}\right)}{\sqrt{3}}$

2.  $\frac{\left(\hat{\mathrm{i}} + \hat{\mathrm{j}} - \hat{\mathrm{k}}\right)}{\sqrt{3}}$

3.  $\frac{\left(\hat{\mathrm{i}} + \hat{\mathrm{j}} + \hat{\mathrm{k}}\right)}{\sqrt{3}}$

4.  $\frac{\left(\hat{\mathrm{i}} - \hat{\mathrm{j}} + \hat{\mathrm{k}}\right)}{\sqrt{3}}$

The forces ${\mathrm{F}}_1 \mathrm{and} {\mathrm{F}}_2$ are acting perpendicular to each other at a point and have resultant R. If force ${\mathrm{F}}_2$ is replaced by $\frac{{\mathrm{R}}^2 - {\mathrm{F}}_1^2}{{\mathrm{F}}_2}$ acting in the direction opposite to that of ${\mathrm{F}}_2$, the magnitude of resultant

(1) Becomes half

(2) Becomes double

(3) Becomes one third

(4) Remains the same

A force of \(20\) N acts on a particle along a direction, making an angle of \(60^\circ\) with the vertical. The component of the force along the vertical direction will be:

If \(\overrightarrow {A}\) $\mathrm{and}$ \(\overrightarrow{B}\) are two vectors inclined to each other at an angle \(\theta,\) then the component of \(\overrightarrow {A}\)$\stackrel{}{}$ perpendicular to \(\overrightarrow {B}\) and lying in the plane containing \(\overrightarrow {A}\) and$$ \(\overrightarrow {B}\) will be:
1. \(\frac{\overrightarrow {A} \overrightarrow{.B}}{B^{2}} \overrightarrow{B}\)
2. \(\overrightarrow{A}   -   \frac{\overrightarrow{A} \overrightarrow{.B}}{B^{2}} \overrightarrow{B}\)
3. \(\overrightarrow{A} -\overrightarrow{B}\)
4. \(\overrightarrow{A} + \overrightarrow{B}\)$\stackrel{}{}$

If \(\left|\overrightarrow A\right|\ne \left|\overrightarrow B\right|\) and \(\left|\overrightarrow A \times \overrightarrow B\right|= \left|\overrightarrow A\cdot \overrightarrow B\right|\), then: