Three blocks \(A\), \(B\) and \(C\) of mass \(3M\), \(2M\) and \(M\) respectively are suspended vertically with the help of springs \({PQ}\) and \({TU}\) and a string \({RS}\) as shown in Figure. The acceleration of blocks \(A\), \(B\) and \(C\) are \(a_{1} , a_{2}~ \text{and}~ a_{3}\) respectively.
                             

The value of acceleration \(a_{1}\) at the moment string \({RS}\) is cut will be: 
1. \(g\) downward
2. \(g\) upward
3. more than \(g\) downward
4. zero

Two bodies of mass, \(4~\text{kg}\) and \(6~\text{kg}\), are tied to the ends of a massless string. The string passes over a pulley, which is frictionless (see figure). The acceleration of the system in terms of acceleration due to gravity (\(g\)) is:

A trolley A has a simple pendulum suspended from a fixed to its desk. A block B is in contact on its vertical side. The trolley is on horizontal rails and accelerates towards the right such that the block is just prevented from falling. The value of the coefficient of friction between A and B is 0.5. The inclination of the pendulum to the vertical is

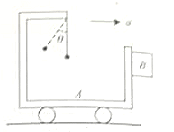
1. ${\tan }^{-1}\left(\frac{1}{2}\right)$

2. ${\tan }^{-1}\left(3\right)$

3. ${\tan }^{-1}\left(\sqrt{2}\right)$

4. ${\tan }^{-1}\left(2\right)$

Figure shows two blocks, each of mass m. The system is released form rest. If accelerations of blocks A and B at any instant (not initially) are ${\mathrm{a}}_1$ and ${\mathrm{a}}_2$, respectively, then

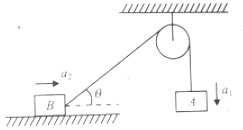
1. ${\mathrm{a}}_1={\mathrm{a}}_2\mathrm{cos\theta }$

2. ${\mathrm{a}}_2={\mathrm{a}}_1\mathrm{cos\theta }$

3. ${\mathrm{a}}_1={\mathrm{a}}_2$

4. None of these

All surface shown in figure are smooth. System is released with the spring unstretched. In equilibrium, compression in the spring will be:

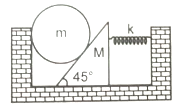
1. $\frac{2mg}{k}$

2. $\frac{\left(M+m\right)g}{\sqrt{2}k}$

3. $\frac{mg}{\sqrt{2}k}$

4. $\frac{mg}{k}$

Two wooden blocks are moving on a smooth horizontal surface such that the mass m remains stationary with respect to block of mass M as shown in the fig. The magnitude of force P is

1. (M + m) g tan $\mathrm{\beta }$

2. g tan $\mathrm{\beta }$

3. (M + m) g cosec $\mathrm{\beta }$

4. mg cos $\mathrm{\beta }$

A solid sphere of mass 2 kg is resting inside a cube as shown in the figure. The cube is moving with a velocity $\mathrm{v} = (5\mathrm{t} \hat{\mathrm{i}} + 2\mathrm{t} \hat{j})$m/s. Here t is the time in second. All surface are smooth. The sphere is at rest with respect to the cube. What is the total force exerted by the sphere on the cube. (Take g = 10 m/s${}^2$)

$1. \sqrt{29} \mathrm{N}$
$2. 29 \mathrm{N}$
$3. 26 \mathrm{N}$
$4. \sqrt{89} \mathrm{N}$
$$

Calculate the reading of the spring balance shown in the figure: (take \(g=10\) m/s²)
                

1. \(60\) N
2. \(40\) N
3. \(50\) N
4. \(80\) N

Calculate the acceleration of the block and trolly system shown in the figure. The coefficient of kinetic friction between the trolly and the surface is 0.05. (g = 10 m/${\mathrm{s}}^2$, the mass of the string is negligible and no other friction exists).

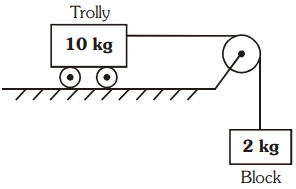
(1) 1.25 m/${\mathrm{s}}^2$

(2) 1.50 m/${\mathrm{s}}^2$

(3) 1.66 m/${\mathrm{s}}^2$

(4) 1.00 m/${\mathrm{s}}^2$

A rocket with a lift-off mass of \(20,000\) \(\mathrm{kg}\) is blasted upwards with an initial acceleration of \(5~\mathrm{ms}^{-2}\). Then initial thrust (force) of the blast is:
(Take \(g=10\) \(\mathrm{ms}^{-2}\))
1. \(7 \times 10^5 \mathrm{~N} \)
2. \(0 \)
3. \(2 \times 10^5 \mathrm{~N} \)
4. \(3 \times 10^5 \mathrm{~N}\)