Two bodies of mass, \(4~\text{kg}\) and \(6~\text{kg}\), are tied to the ends of a massless string. The string passes over a pulley, which is frictionless (see figure). The acceleration of the system in terms of acceleration due to gravity (\(g\)) is:

1.
\(\dfrac{g}{2}\)
2.
\(\dfrac{g}{5}\)
3.
\(\dfrac{g}{10}\)
4.
\(g\)

Calculate the acceleration of the block and trolly system shown in the figure. The coefficient of kinetic friction between the trolly and the surface is 0.05. (g = 10 m/, the mass of the string is negligible and no other friction exists).
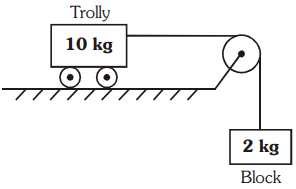
(1) 1.25 m/
(2) 1.50 m/
(3) 1.66 m/
(4) 1.00 m/
A rocket with a lift-off mass of \(20,000\) \(\mathrm{kg}\) is blasted upwards with an initial acceleration of \(5~\mathrm{ms}^{-2}\). Then initial thrust (force) of the blast is:
(Take \(g=10\) \(\mathrm{ms}^{-2}\))
1. \(7 \times 10^5 \mathrm{~N} \)
2. \(0 \)
3. \(2 \times 10^5 \mathrm{~N} \)
4. \(3 \times 10^5 \mathrm{~N}\)
Two masses \(8~\text{kg}\) and \(12~\text{kg}\) are connected at the two ends of a light inextensible string that goes over a frictionless pulley. The acceleration of the masses and the tension in the string when the masses are released are:
1. \(2~\text{ms}^{-2}, 69~\text{N}\)
2. \(1~\text{ms}^{-2}, 69~\text{N}\)
3. \(2~\text{ms}^{-2}, 96~\text{N}\)
4. \(1~\text{ms}^{-2}, 96~\text{N}\)
A batsman deflects a ball of mass 0.15 kg by an angle of 45° without changing its initial speed which is equal to 54 km/h. Then impulse imparted to the ball is:
1. \(5.2~\mathrm{kgms}^{-1}\)
2. \(3.2~\mathrm{kgms}^{-1}\)
3. \(2.2~\mathrm{kgms}^{-1}\)
4. \(4.2~ \mathrm{kgms}^{-1}\)
The figure shows the position-time graph of a body of mass \(0.04~\text{kg}\). Then the magnitude of each impulse is:
1. \(8 \times 10^{-4} ~\text{kg-ms}^{-1}\)
2. \(8 \times 10^{-3} ~\text{kg-ms}^{-1}\)
3. \(4 \times 10^{-4} ~\text{kg-ms}^{-1}\)
4. \(4 \times 10^{-3} ~\text{kg-ms}^{-1}\)
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 m/s. How long does the body take to stop?
1. 6 sec
2. 5 sec
3. 7 sec
4. 4 sec
A constant force acting on a body of mass \(3.0\) kg changes its speed from \(2.0\) m/s to \(3.5\) m/s in \(25\) s. The direction of the motion of the body remains unchanged. What is the magnitude and direction of the force?
| 1. | \(0.18\) N opposite to the direction of motion. |
| 2. | \(0.18\) N along the direction of motion. |
| 3. | \(0.16\) N along the direction of motion. |
| 4. | \(0.16\) N opposite to the direction of motion. |
A body of mass \(5\) kg is acted upon by two perpendicular forces, \(8\) N and \(6\) N. The magnitude of the acceleration of the body is:
| 1. | \(0.99\) ms–2 | 2. | \(3\) ms–2 |
| 3. | \(2\) ms–2 | 4. | \(0.77\) ms–2 |
The driver of a three-wheeler moving with a speed of \(36~\text{km/h}\) sees a child standing in the middle of the road and brings his vehicle to rest in \(4.0~\text{s}\) just in time to save the child. What is the average retarding force on the vehicle?
(The mass of the three-wheeler is \(400~\text{kg}\) and the mass of the driver is \(65~\text{kg}\).)
1. \(7.1 \times 10^4 ~\text{N}\)
2. \(2.1 \times 10^4 ~\text{N}\)
3. \(1.7 \times 10^3 ~\text{N}\)
4. \(1.2 \times 10^3 ~\text{N}\)







