Two particles of mass \(5~\text{kg}\) and \(10~\text{kg}\) respectively are attached to the two ends of a rigid rod of length \(1~\text{m}\) with negligible mass. The centre of mass of the system from the \(5~\text{kg}\) particle is nearly at a distance of:
1. \(50~\text{cm}\)
2. \(67~\text{cm}\)
3. \(80~\text{cm}\)
4. \(33~\text{cm}\)
1. \(50~\text{cm}\)
2. \(67~\text{cm}\)
3. \(80~\text{cm}\)
4. \(33~\text{cm}\)
What would be the torque about the origin when a force \(3\hat{j}~\text N\) acts on a particle whose position vector is \(2\hat{k}~\text m?\)
| 1. | \(6\hat{j}~\text{N-m}\) | 2. | \(-6\hat{i}~\text{N-m}\) |
| 3. | \(6\hat{k}~\text{N-m}\) | 4. | \(6\hat{i}~\text{N-m}\) |
The angular speed of the wheel of a vehicle is increased from 360 rpm to 1200 rpm in 14 seconds. Its angular acceleration is
\(1.~2\pi ~rad/s^{2}\)
\(2.~28\pi ~rad/s^{2}\)
\(3.~120\pi ~rad/s^{2}\)
\(4.~\pi ~rad/s^{2}\)
Three identical spheres, each of mass M, are placed at the corners of a right-angle triangle with mutually perpendicular sides equal to 2 m (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of the center of mass.
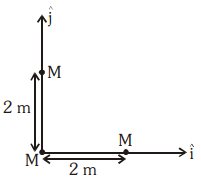
1.
2.
3.
4.
In the \(\mathrm{HCl}\) molecule, the separation between the nuclei of the two atoms is about \(1.27~\mathring{\text A}~(1~\mathring{\text A}=10^{10}~\text m).\) Then the approximate location of the CM of the molecule is:
(Given that a chlorine atom is about \(35.5\) times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus).
| 1. | \(1.235~\mathring{\text A}\) from \(\mathrm{H-}\)atom |
| 2. | \(2.41~\mathring{\text A}\) from \(\mathrm{Cl-}\)atom |
| 3. | \(3.40~\mathring{\text A}\) from \(\mathrm{Cl-}\)atom |
| 4. | \(1.07~\mathring{\text A}\) from \(\mathrm{H-}\)atom |
A child sits stationary at one end of a long trolley moving uniformly with a speed \(v\) on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, then the speed of the centre of mass of the (trolley + child) system:
1. decreases
2. increases
3. remains unchanged
4. none of these
A non-uniform bar of weight \(W\) is suspended at rest by two strings of negligible weight as shown in the figure. The angles made by the strings with the vertical are \(36.9^\circ\) and \(53.1^\circ\) respectively. The bar is \(2\) m long. The distance \(d\) of the center of gravity of the bar from its left end is:
(Take sin\(36.9^\circ=0.6\) and sin\(53.1^\circ=0.8\))
1. \(69\) cm
2. \(72\) cm
3. \(79\) cm
4. \(65\) cm
A car weighs \(1800~\text{kg}.\) The distance between its front and back axles is \(1.8~\text m.\) Its center of gravity is \(1.05~\text m,\) behind the front axle. The force exerted by the level ground on each front wheel and each back wheel is respectively:
1. \(2680~\text N, ~5145~\text N\)
2. \(5145~\text N, ~3675~\text N\)
3. \(5145~\text N, ~5145~\text N\)
4. \(3675~\text N, ~5145~\text N\)
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. The angular velocity of the solid sphere is:
| 1. | more than the angular velocity of the hollow cylinder. |
| 2. | less than the angular velocity of the hollow cylinder. |
| 3. | equal to the angular velocity of the hollow cylinder. |
| 4. | none of these. |
A solid cylinder of mass \(20\) kg rotates about its axis with angular speed \(100\) rad s-1. The radius of the cylinder is \(0.25\) m. The kinetic energy associated with the rotation of the cylinder is:
1. \(3000\) J
2. \(3125\) J
3. \(2528\) J
4. \(2100\) J







