The figure shows a man of mass \(65\) kg standing stationary with respect to a horizontal conveyor belt that is accelerating with \(1\) ms-2. If the coefficient of static friction between the man’s shoes and the belt is \(0.2,\) up to what acceleration of the belt can the man continue to be stationary relative to the belt? (Take \(g=10\) m/s2)

1.
\(2\) ms-2
2.
\(3\) ms-2
3.
\(1\) ms-2
4.
\(9.8\) ms-2

| 1. | \(2\) ms-2 | 2. | \(3\) ms-2 |
| 3. | \(1\) ms-2 | 4. | \(9.8\) ms-2 |
| Lowest point | Highest point | |
| 1. | \(mg-T_1\) | \(mg+T_2\) |
| 2. | \(mg+T_1\) | \(mg+T_2\) |
| 3. | ||
| 4. |
(\(T_1\) and \(v_1\) denote the tension and speed at the lowest point. \(T_2\) and \(v_2\) denote corresponding values at the highest point.)
A helicopter of mass 1000 kg rises with a vertical acceleration of . The crew and the passengers weigh 300 kg. The magnitude and direction of the action of the rotor of the helicopter on the surrounding air are:
A stream of water flowing horizontally with a speed of \(15\) ms–1 pushes out of a tube of cross-sectional area \(10^{-2}\) m2 and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water, assuming it does not rebound? (Density of water, \(\rho=10^{3}\) kg-m–3)
| 1. | \(1500\) N | 2. | \(2250\) N |
| 3. | \(1650\) N | 4. | \(2200\) N |
An aircraft executes a horizontal loop at a speed of \(720\) km/h with its wings banked at \(15^{\circ}\). What is the radius of the loop? (Take \(g=10~\text{m/s}^{2}\), \(\tan 15^{\circ}=0.27\))
1. \(1.30\) km
2. \(14.9\) km
3. \(1.55\) km
4. \(20.9\) km
A train runs along an unbanked circular track of radius \(30\) m at a speed of \(54\) km/h. The mass of the train is \(10^{6}\) kg. What is the angle of banking required to prevent wearing out of the rail?
| 1. | \(30^\circ\) | 2. | \(45^\circ\) |
| 3. | \(53^\circ\) | 4. | \(37^\circ\) |
A monkey of mass \(40\) kg climbs on a massless rope (as shown in the figure) which can stand a maximum tension of \(600\) N. In which of the following cases will the rope break?
| 1. | the monkey climbs up with an acceleration of \(6 \mathrm{~ms}^{-2}\). |
| 2. | the monkey climbs down with an acceleration of \(4 \mathrm{~ms}^{-2}\). |
| 3. | the monkey climbs up with a uniform speed of \(5 \mathrm{~ms}^{-2}\) |
| 4. | the monkey falls down the rope nearly freely under gravity. |
The rear side of a truck is open and a box of 40 kg mass is placed 5 m away from the open end as shown in Figure. The coefficient of friction between the box and the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with . At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).
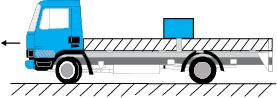
1. 15.5 m
2. 40.5 m
3. 18.8 m
4. 25.0 m
What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is \(25\) m?
1. \(16.7\) m/s
2. \(15.8\) m/s
3. \(35\) m/s
4. \(24\) m/s
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 revs/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
1. 3.14 rad/s
2. 4.17 rad/s
3. 4.71 rad/s
4. 3.21 rad/s



