A \(600~\text{pF}\) capacitor is charged by a \(200~\text V\) supply. It is then disconnected from the supply and is connected to another uncharged \(600~\text{pF}\) capacitor. How much electrostatic energy is lost in the process?
1. \( 5 \times 10^{-6} ~\text J\)
2. \( 6 \times 10^{-5} ~\text J\)
3. \( 6 \times 10^{-6} ~\text J\)
4. \( 5 \times 10^{-5}~\text J\)
1. \( 5 \times 10^{-6} ~\text J\)
2. \( 6 \times 10^{-5} ~\text J\)
3. \( 6 \times 10^{-6} ~\text J\)
4. \( 5 \times 10^{-5}~\text J\)
A charge of \(8~\text{mC}\) is located at the origin. The work done in taking a small charge of \(-2\times 10^{-9}~\text C\) from a point \(P (0, 0, 3~\text{cm})\) to a point \(Q (0, 4~\text{cm}, 0),\) via a point \(R (0, 6~\text{cm}, 9~\text{cm})\) is:
1. \(3.27~\text J\)
2. \(1.27~\text J\)
3. \(0.27~\text J\)
4. \(2.70~\text J\)
A cube of side \(b\) has a charge \(q\) at each of its vertices. The potential due to this charge array at the center of the cube is:
| 1. | \(\dfrac{4q}{\sqrt3\pi\varepsilon_0b}\) | 2. | \(\dfrac{8q}{\sqrt3\pi\varepsilon_0b}\) |
| 3. | \(\dfrac{2q}{\sqrt3\pi\varepsilon_0b}\) | 4. | Zero |
Two tiny spheres carrying charges of \(1.5\) µC and \(2.5\) µC are located \(30\) cm apart. What is the potential at a point \(10\) cm from the midpoint in a plane normal to the line and passing through the mid-point?
| 1. | \(1.5\times 10^{5}\) V | 2. | \(1.0\times 10^{5}\) V |
| 3. | \(2.4\times 10^{5}\) V | 4. | \(2.0\times 10^{5}\) V |
(taking the zero of the potential energy at an infinite separation of the electron from the proton.)
1. \(-23.1~\text{eV}\)
2. \(27.0~\text{eV}\)
3. \(-27.2~\text{eV}\)
4. \(23.7~\text{eV}\)
Two charged conducting spheres of radii \(a\) and \(b\) are connected to each other by a wire. The ratio of electric fields at the surfaces of the two spheres is:
| 1. | \(\dfrac{a}{b}\) | 2. | \(1\) |
| 3. | \(\dfrac{2a}{b}\) | 4. | \(\dfrac{b}{a}\) |
What is the area of the plates of a \(2~\text{F}\) parallel plate capacitor, given that the separation between the plates is \(0.5~\text{cm}\)?
1. \(1100~\text{km}^2\)
2. \(1130~\text{km}^2\)
3. \(1110~\text{km}^2\)
4. \(1105~\text{km}^2\)
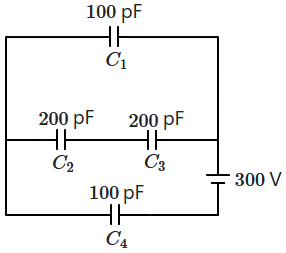
The equivalent capacitance of the circuit is:
| 1. | \(200~\text{pF}\) | 2. | \(\dfrac{200}{3}~\text{pF}\) |
| 3. | \(200~\mu\text{F}\) | 4. | \(150~\text{pF}\) |
1. \(1.7\times10^{-6}~\text J\)
2. \(2.12\times10^{-6}~\text J\)
3. \(2.55\times10^{-6}~\text J\)
4. \(1.66\times10^{-6}~\text J\)
A \(4 ~\mu \text{F}\) capacitor is charged by a \(200 ~\text {V}\) supply. It is then disconnected from the supply and is connected to another uncharged \(2 ~\mu \text{F}\) capacitor. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation?
1. \(3.10 \times 10^{-2} ~\text {J}\)
2. \(3.33 \times 10^{-3} ~\text {J}\)
3. \(1.23 \times 10^{-2} ~\text {J}\)
4. \(2.67 \times 10^{-2} ~\text {J}\)