KE acquired by a mass m intravelling a certain distance d, starting from rest, under the action of a constant force F is

1. Directly proportional to $\sqrt{\mathrm{m}}$

2. Directly proportional to m

3. Directly proportional to $\frac{1}{\mathrm{m}}$

4. None of these

The total work done on a particle is equal to the change in its kinetic energy. This is applicable 

1. Always

2. Only if the conservative forces are acting on it

3. Only in inertial frames

4. Only when pseudo forces are absent

A particle of mass 0.1 kg is subjected to a force which varies with distance as shown. If it starts its journey from rest at x=0, then its velocity at x=12 m is

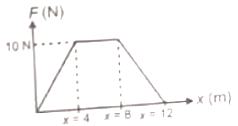
1. 0 m/s

2. $20\sqrt{2}$m/s

3. $20\sqrt{3}$m/s

4. 40 m/s

Potential energy is defined:

A stick of mass m and length l is pivoted at one end and is displaced through an angle $\mathrm{\theta }$. The increase in potential energy is 

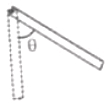
1. $\mathrm{mg}\frac{\mathrm{l}}{2}(1-\mathrm{cos\theta })$

2. $\mathrm{mg}\frac{\mathrm{l}}{2}(1+\mathrm{cos\theta })$

3. $\mathrm{mg}\frac{\mathrm{l}}{2}(1-\mathrm{sin\theta })$

4. $\mathrm{mg}\frac{\mathrm{l}}{2}(1+\mathrm{sin\theta })$

A spring with spring constants k when compressed by 1 cm, the potential energy stored is U. If it is further compressed by 3 cm, then change in its potential energy is

1. 3U

2. 9U

3. 8U

4. 15U

Two springs have force constant K₁ and K₂ (K₁>K₂). Each spring is extended by same force F. If their elastic potential energy are E₁ and E₂ then $\frac{{\mathrm{E}}_1}{{\mathrm{E}}_2}$ is

1. $\frac{{\mathrm{K}}_1}{{\mathrm{K}}_2}$

2. $\frac{{\mathrm{K}}_2}{{\mathrm{K}}_1}$

3. $\sqrt{\frac{{\mathrm{K}}_1}{{\mathrm{K}}_2}}$

4. $\sqrt{\frac{{\mathrm{K}}_2}{{\mathrm{K}}_1}}$

Initially mass m is held such that spring is in relaxed condition. If mass m is suddenly released, maximum elongation in spring will be

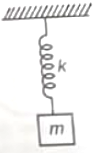
1. $\frac{\mathrm{mg}}{\mathrm{k}}$

2. $\frac{2\mathrm{mg}}{\mathrm{k}}$

3. $\frac{\mathrm{mg}}{2\mathrm{k}}$

4. $\frac{\mathrm{mg}}{4\mathrm{k}}$

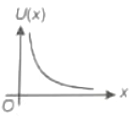
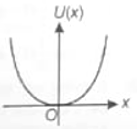
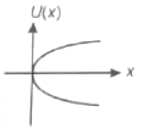
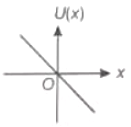
On a particle placed at origin a variable force $\mathrm{F}=-\mathrm{ax}$ (where a is a positive constant) is applied. If $\mathrm{U}\left(0\right)=0$, the graph between potential energy of particle U(x) and x is best represented by

1. 

2. 

3. 

4. 

The variation of potential energy U of a body moving along x-axis varies with its position (x) as shown in figure

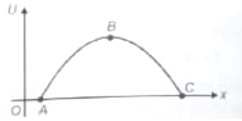
The body is in equilibrium state at

1. A

2. B

3. C

4. Both A & C