Potential energy is defined:
1.
Only in conservative fields
2.
As the negative of the work done by conservative forces
3.
As the negative of the work done by external forces when \(\Delta K=0\)
4.
All of these
A stick of mass m and length l is pivoted at one end and is displaced through an angle . The increase in potential energy is
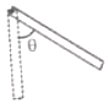
1.
2.
3.
4.
A spring with spring constants k when compressed by 1 cm, the potential energy stored is U. If it is further compressed by 3 cm, then change in its potential energy is
1. 3U
2. 9U
3. 8U
4. 15U
Two springs have force constant K1 and K2 (K1>K2). Each spring is extended by same force F. If their elastic potential energy are E1 and E2 then is
1.
2.
3.
4.
Initially mass m is held such that spring is in relaxed condition. If mass m is suddenly released, maximum elongation in spring will be
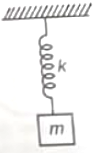
1.
2.
3.
4.
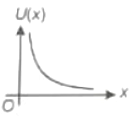
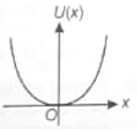
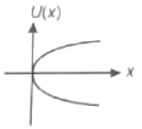
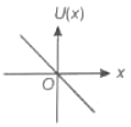
On a particle placed at origin a variable force (where a is a positive constant) is applied. If , the graph between potential energy of particle U(x) and x is best represented by
1. 
2. 
3. 
4. 
The variation of potential energy U of a body moving along x-axis varies with its position (x) as shown in figure
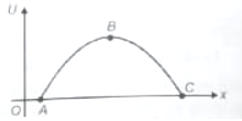
The body is in equilibrium state at
1. A
2. B
3. C
4. Both A & C
A uniform chain of length L and mass M is lying on a smooth table and one third of its length is hanging vertically down over the edge of the table. If g is acceleration due to gravity, the minimum work required to pull the hanging part of the chain on the table is
1. MgL
2.
3.
4.
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is
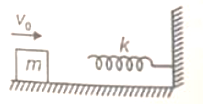
1.
2.
3.
4.
For a particle moving under the action of a variable force, kinetic energy-position graph is given, then
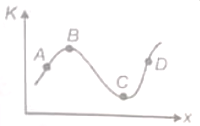
1. At A particle is decelerating
2. At B particle is accelerating
3. At C particle has maximum velocity
4. At D particle has maximum acceleration






