If in a plano-convex lens, the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm, the refractive index of the material of the lens will be:

(1) 1.5

(2) 1.66

(3) 1.33

(4) 3

A glass concave lens is placed in a liquid in which it behaves like a convergent lens. If the refractive indices of glass and liquid with respect to air are ${}_a{\mu }_g$ and ${}_a{\mu }_l$ respectively, then

(1) ${}_a{\mu }_g$ = 5${}_a{\mu }_l$

(2) ${}_a{\mu }_g$ > ${}_a{\mu }_l$

(3) ${}_a{\mu }_g$ < ${}_a{\mu }_l$

(4) ${}_a{\mu }_g$ = 2${}_a{\mu }_l$

The diameter of the aperture of a plano-convex lens is 6 cm and its maximum thickness is 3 mm. If the velocity of light in the material of the lens is 2 x 10⁸ m/s, its focal length is (approximately):

(1) 10 cm

(2) 15 cm

(3) 30 cm

(4) 60 cm

Two plano-convex lenses of equal focal lengths are arranged as shown.

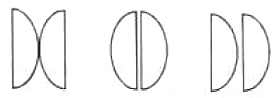
The ratio of the combined focal lengths is:

(1) 1: 2: 1

(2) 1: 2: 3

(3) 1: 1: 1

(4) 2: 1: 2

When an object is at a distance of u₁ and u₂ from a lens, a real image and a virtual image is formed respectively having the same magnification. The focal length of the lens is:

(1) $u_1-u_2$

(2) $\frac{u_1-u_2}{2}$

(3) $\frac{u_1+u_2}{2}$

(4) $u_1+u_2$

A concave lens of focal length f produces an image (1/x) of the size of the object. The distance of the object from the lens is:

(1) (x - 1)f

(2) (x + 1)f

(3) {(x - 1)/x}f

(4) {(x + 1)/x}f

A thin equiconvex glass lens of refractive index 1.5 has a power of 5D. When the lens is immersed in a liquid of refractive index $\mathrm{\mu }$, it acts as a divergent lens of focal length 100 cm. The value of $\mathrm{\mu }$ of liquid is:

(1) 4 / 3

(2) 3 / 4

(3) 5 / 3

(4) 8 / 3

In the case of the displacement method of lenses, the product of magnification in both cases is:

(1) 1

(2) 2

(3) Zero

(4) Infinite

In the displacement method, a convex lens is placed in between an object and a screen. If the magnifications in the two positions are m₁ and m₂ and the displacement of the lens between the two positions is x, then the focal length of the lens is:

(1) $\frac{x}{m_1+m_2}$

(2) $\frac{x}{m_1-m_2}$

(3) $\frac{x}{{\left(m_1+m_2\right)}^2}$

(4) $\frac{x}{{\left(m_1-m_2\right)}^2}$

The focal length of a planoconvex glass lens is 20 cm $\left({\mu }_0=1.5\right)$. The plane face of it is silvered. An illuminating object is placed at a distance of 60 cm from the lens on its axis along the convex side. Then the distance (in cm) of the image is:

(1) 20

(2) 30

(3) 40

(4) 12