The minimum and maximum distances of a planet revolving around the sun are \(r\) and \(R.\) If the minimum speed of the planet on its trajectory is \(v_0,\) its maximum speed will be:

1.	\(\dfrac{v_0R}{r}\)	2.	\(\dfrac{v_0r}{R}\)
3.	\(\dfrac{v_0R^2}{r^2}\)	4.	\(\dfrac{v_0r^2}{R^2}\)

The torque on a planet about the centre of the sun is:

1. zero.

2. negative.

3. positive.

4. dependent on the mass of the planet.

During the motion of a planet from perihelion to aphelion, the work done by the gravitational force of the sun on it is:

1. zero.

2. negative.

3. positive.

4. may be positive or negative.

The time period of a satellite in a circular orbit of radius R is T. The period of another satellite in a circular orbit of radius 4R is:

1. 4T

2. $\frac{\mathrm{T}}{4}$

3. 8T

4. $\frac{\mathrm{T}}{8}$

Gravitation is the phenomenon of interaction between:

1. Point masses only

2. Any arbitrarily shaped masses

3. Planets only

4. None of these

The Force of gravitation between two masses is found to be F in a vacuum. If both the masses are dipped in water at the same distance, then the new force will be:

1. >F

2. <F

3. F

4. Cannot say

Two-point masses m and 4m are separated by a distance d on a line. A third point mass m₀ is to be placed at a point on the line such that the net gravitational force on it is equal to zero.

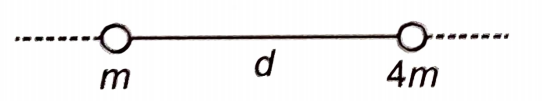
The distance of that point from the mass m is:

1. $\frac{\mathrm{d}}{2}$

2. $\frac{\mathrm{d}}{4}$

3. $\frac{\mathrm{d}}{3}$

4. $\frac{\mathrm{d}}{5}$

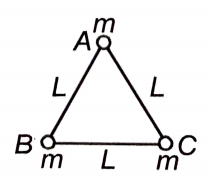
Three particles A, B and C, each of mass m are lying at the corners of an equilateral triangle of side L. If particle A is released keeping the particles B and C fixed, the magnitude of the instantaneous acceleration of A is:

1. $\sqrt{3}\frac{{\mathrm{Gm}}^2}{{\mathrm{L}}^2}$

2. $\sqrt{2}\frac{{\mathrm{Gm}}^2}{{\mathrm{L}}^2}$

3. $\sqrt{2}\frac{\mathrm{Gm}}{{\mathrm{L}}^2}$

4. $\sqrt{3}\frac{\mathrm{Gm}}{{\mathrm{L}}^2}$

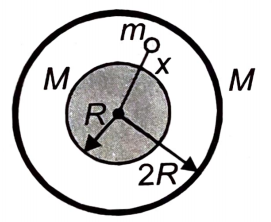
A uniform sphere of mass M and radius R is surrounded by a concentric spherical shell of the same mass but radius 2R. A point mass m is kept at a distance x (>R) in the region bounded by the spheres as shown in the figure. The net gravitational force on that particle is:

1. $\frac{\mathrm{GMm}}{{\mathrm{x}}^2}$

2. $\frac{\mathrm{GMmx}}{{\mathrm{R}}^3}$

3. $\frac{\mathrm{G}(\mathrm{M}+\mathrm{m})}{{\mathrm{x}}^2}$

4. Zero

The gravitational constant depends upon:

1. Size of the bodies

2. Gravitational masses

3. Distance between the bodies

4. None of these