As we go from the equator to the poles, the value of 'g':

1. Remains the same

2. Decreases

3. Increases

4. First increase and then decrease

What should be the angular speed with which the earth has to rotate on its axis so that a person on the equator would weigh $\frac{3}{5}$th as much as he weighs at present?

1. $\sqrt{\frac{2\mathrm{g}}{5\mathrm{R}}}$

2. $\sqrt{\frac{2\mathrm{R}}{5\mathrm{g}}}$

3. $\frac{2\sqrt{\mathrm{R}}}{\sqrt{5\mathrm{g}}}$

4. $\frac{2\mathrm{g}}{5\mathrm{R}}$

The acceleration due to gravity on a planet is 1.96 m/s². If it is safe to jump from a height of 3 m on the earth, the corresponding height on the planet will be:

1. 3 m

2. 6 m

3. 9 m

4. 15 m

An object is taken to height 2R above the surface of the earth, the increase in potential energy is: [R is the radius of the earth]

1. $\frac{\mathrm{mgR}}{2}$

2. $\frac{\mathrm{mgR}}{3}$

3. $\frac{2\mathrm{mgR}}{3}$

4. $2 \mathrm{mgR}$

The change in potential energy when a body of mass m is raised to height nR from the earth's surface is: (R is the radius of the earth)

1. $\mathrm{mgR} \left(\frac{\mathrm{n}}{\mathrm{n}-1}\right)$

2. $\mathrm{nmgR}$

3. $\mathrm{mgR}\left(\frac{\mathrm{n}}{\mathrm{n}+1}\right)$

4. $\mathrm{mgR}\left(\frac{{\mathrm{n}}^2}{{\mathrm{n}}^2+1}\right)$

A stationary object is released from a point P at a distance of 3R from the centre of the moon which has radius R and mass M. Which of the following gives the speed of the object on hitting the moon?

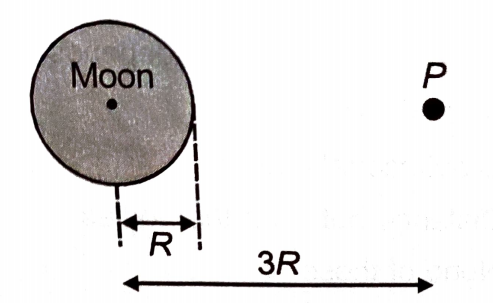
1. ${\left(\frac{2\mathrm{GM}}{3\mathrm{R}}\right)}^{1/2}$

2. ${\left(\frac{4\mathrm{GM}}{3\mathrm{R}}\right)}^{1/2}$

3. ${\left(\frac{\mathrm{GM}}{3\mathrm{R}}\right)}^{1/2}$

4. ${\left(\frac{\mathrm{GM}}{\mathrm{R}}\right)}^{1/2}$

Four particles A, B, C and D, each of mass m, are kept at the corners of a square of side L. Now the particle D is taken to infinity by an external agent keeping the other particles fixed with their respective positions. The work done by the gravitational force acting on the particle D during its movement is:

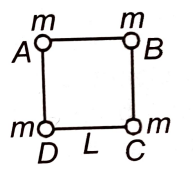
1. $2\frac{{\mathrm{Gm}}^2}{\mathrm{L}}$

2. $-2\frac{{\mathrm{Gm}}^2}{\mathrm{L}}$

3. $\frac{{\mathrm{Gm}}^2}{\mathrm{L}}\left(\frac{2\sqrt{2}+1}{\sqrt{2}}\right)$

4. $-\frac{{\mathrm{Gm}}^2}{\mathrm{L}}\left(\frac{2\sqrt{2}+1}{\sqrt{2}}\right)$

If an object is projected vertically upward with a speed equal to half the escape velocity on earth, then the maximum height attained by it is: [R is radius of earth]

1. R

2. $\frac{\mathrm{R}}{2}$

3. 2R

4. $\frac{\mathrm{R}}{3}$

If a satellite of mass \(400\) kg revolves around the earth in an orbit with a speed of \(200\) m/s, then its potential energy is:
1. \(-1.2\) MJ
2. \(-8.0\) MJ
3. \(-16\) MJ
4. \(-2.4\) MJ

An artificial satellite revolves around a planet for which gravitational force \((F)\) varies with the distance \(r\) from its centre as \(F \propto r^{2}.\) If \(v_0\) is its orbital speed, then: