An object is taken to height 2R above the surface of the earth, the increase in potential energy is: [R is the radius of the earth]

1. $\frac{\mathrm{mgR}}{2}$

2. $\frac{\mathrm{mgR}}{3}$

3. $\frac{2\mathrm{mgR}}{3}$

4. $2 \mathrm{mgR}$

The change in potential energy when a body of mass m is raised to height nR from the earth's surface is: (R is the radius of the earth)

1. $\mathrm{mgR} \left(\frac{\mathrm{n}}{\mathrm{n}-1}\right)$

2. $\mathrm{nmgR}$

3. $\mathrm{mgR}\left(\frac{\mathrm{n}}{\mathrm{n}+1}\right)$

4. $\mathrm{mgR}\left(\frac{{\mathrm{n}}^2}{{\mathrm{n}}^2+1}\right)$

A stationary object is released from a point P at a distance of 3R from the centre of the moon which has radius R and mass M. Which of the following gives the speed of the object on hitting the moon?

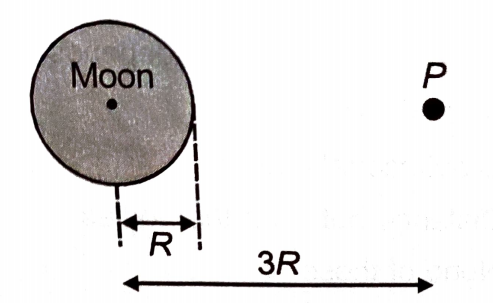
1. ${\left(\frac{2\mathrm{GM}}{3\mathrm{R}}\right)}^{1/2}$

2. ${\left(\frac{4\mathrm{GM}}{3\mathrm{R}}\right)}^{1/2}$

3. ${\left(\frac{\mathrm{GM}}{3\mathrm{R}}\right)}^{1/2}$

4. ${\left(\frac{\mathrm{GM}}{\mathrm{R}}\right)}^{1/2}$

Four particles A, B, C and D, each of mass m, are kept at the corners of a square of side L. Now the particle D is taken to infinity by an external agent keeping the other particles fixed with their respective positions. The work done by the gravitational force acting on the particle D during its movement is:

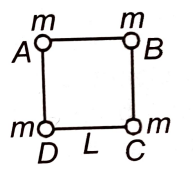
1. $2\frac{{\mathrm{Gm}}^2}{\mathrm{L}}$

2. $-2\frac{{\mathrm{Gm}}^2}{\mathrm{L}}$

3. $\frac{{\mathrm{Gm}}^2}{\mathrm{L}}\left(\frac{2\sqrt{2}+1}{\sqrt{2}}\right)$

4. $-\frac{{\mathrm{Gm}}^2}{\mathrm{L}}\left(\frac{2\sqrt{2}+1}{\sqrt{2}}\right)$

If an object is projected vertically upward with a speed equal to half the escape velocity on earth, then the maximum height attained by it is: [R is radius of earth]

1. R

2. $\frac{\mathrm{R}}{2}$

3. 2R

4. $\frac{\mathrm{R}}{3}$

If a satellite of mass \(400\) kg revolves around the earth in an orbit with a speed of \(200\) m/s, then its potential energy is:
1. \(-1.2\) MJ
2. \(-8.0\) MJ
3. \(-16\) MJ
4. \(-2.4\) MJ

An artificial satellite revolves around a planet for which gravitational force \((F)\) varies with the distance \(r\) from its centre as \(F \propto r^{2}.\) If \(v_0\) is its orbital speed, then:

If the gravitational potential on the surface of the earth is V₀, then the potential at a point at a height equal to half of the radius of the earth is:

1. $\frac{{\mathrm{V}}_0}{2}$

2. $\frac{2}{3}{\mathrm{V}}_0$

3. $\frac{{\mathrm{V}}_0}{3}$

4. $\frac{3{\mathrm{V}}_0}{2}$

The total mechanical energy of an object of mass m projected from the surface of the earth with escape speed is:

1. Zero

2. Infinite

3. $-\frac{\mathrm{GMm}}{2\mathrm{R}}$

4. $-\frac{\mathrm{GMm}}{3\mathrm{R}}$

A body is thrown with a velocity equal to n times the escape velocity (v_e). The velocity of the body at a large distance away will be:

1. ${\mathrm{v}}_{\mathrm{e}}\sqrt{{\mathrm{n}}^2-1}$

2. ${\mathrm{v}}_{\mathrm{e}}\sqrt{{\mathrm{n}}^2+1}$

3. ${\mathrm{v}}_{\mathrm{e}}\sqrt{1-{\mathrm{n}}^2}$

4. None of these