Consider a cycle followed by an engine (figure). 

1 to 2 is isothermal,
2 to 3 is adiabatic,
3 to 1 is adiabatic.
Such a process does not exist, because:

(a)	heat is completely converted to mechanical energy in such a process, which is not possible.
(b)	In this process, mechanical energy is completely converted to heat, which is not possible.
(c)	curves representing two adiabatic processes don’t intersect.
(d)	curves representing an adiabatic process and an isothermal process don't intersect.

Choose the correct alternatives:

1.	(a), (b)	2.	(a), (c)
3.	(b), (c)	4.	(c), (d)

Consider a heat engine as shown in the figure. ${\mathrm{Q}}_1 \mathrm{and} {\mathrm{Q}}_2$ are heat added to ${\mathrm{T}}_1$ and heat taken from ${\mathrm{T}}_2$ respectively, in one cycle of the engine. W is the mechanical work done on the engine.

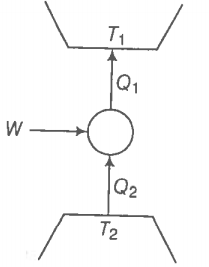
If W > 0, then possibilities are:

$(a) {\mathrm{Q}}_1>{\mathrm{Q}}_2>0(b) {\mathrm{Q}}_2>{\mathrm{Q}}_1>0(c) {\mathrm{Q}}_2<{\mathrm{Q}}_1<0(d) {\mathrm{Q}}_1<0, {\mathrm{Q}}_2>0$

Choose the correct alternatives:
1. (b, c)

2. (a, d)

3. (b, d)

4. (a, c)

Q. 5 Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of the final pressure of gas in B to that of gas in A is:

a. $2^{\gamma -1}$

b. ${\left(\frac{1}{2}\right)}^{\gamma -1}$

c. ${\left(\frac{1}{1-\gamma }\right)}^2$

d. ${\left(\frac{1}{\gamma -1}\right)}^2$

The figure shows the \((P\text-V)\) diagram of an ideal gas undergoing a change of state from \(A\) to \(B\). Four different paths \(\mathrm{I, II, III}\) and \(\mathrm{IV}\), as shown in the figure, may lead to the same change of state.
               

 
Which of the following options contains only correct statements?
1. (b), (c), (d)
2. (a), (d)
3. (b), (c)
4. (a), (c), (d)

1. \(T = \dfrac{T_{1} + T_{2} + T_{3}}{3}\)

2. \(T = \dfrac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{M_{1} + M_{2} + M_{3}}\)

3. \(T = \dfrac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{3 \left(\right. M_{1} + M_{2} + M_{3} \left.\right)}\)

4. \(T = \dfrac{M_{1} T_{1} s + M_{2} T_{2} s + M_{3} T_{3} s}{M_{1} + M_{2} + M_{3}}\)

Consider the \((P\text-V)\) diagram for an ideal gas shown in the figure.

1.		2.
3.		4.

If an average person jogs, he produces \(14.5 \times10^3\) cal/min. This is removed by the evaporation of sweat. The amount of sweat evaporated per minute (assuming \(1\) kg requires \(580 \times10^3\) cal for evaporation) is:

An ideal gas undergoes four different processes from the same initial state (figure). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of \(1,\) \(2,\) \(3\) and \(4,\) which one is adiabatic?