The motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is
(a)
simple harmonic motion
(b)
non-periodic motion
(c)
periodic motion
(d)
periodic but not SHM
Choose the correct alternatives:
1. (a), (c)
2. (a), (d)
3. (c), (d)
4. (b), (c)
1. (a), (c)
2. (a), (d)
3. (c), (d)
4. (b), (c)
The rotation of the earth about its axis is:
| (a) | periodic motion |
| (b) | simple harmonic motion |
| (c) | periodic but not simple harmonic motion |
| (d) | non-periodic motion |
Choose the correct alternatives:
1. (a), (b), (d)
2. (a), (c)
3. (b), (d)
4. (c), (d)
A body is performing SHM, then its:
| (a) | average total energy per cycle is equal to its maximum kinetic energy. |
| (b) | average kinetic energy per cycle is equal to half of its maximum kinetic energy. |
| (c) | mean velocity for a complete cycle is equal to \(\dfrac{2}{\pi}\) times of its maximum velocity. |
| (d) | root mean square velocity is \(\dfrac{1}{\sqrt{2}}\) times of its maximum velocity. |
Choose the correct alternatives:
1. (a), (b), (d)
2. (a), (c)
3. (b), (d)
4. (b), (c), (d)
The (displacement-time) graph of a particle executing SHM is shown in the figure. Then:
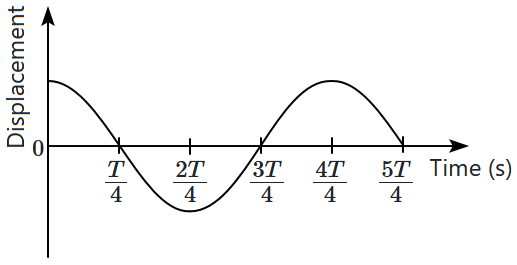
| (a) | the force is zero at \(t=\dfrac{3T}{4}\) |
| (b) | the acceleration is maximum at \(t=\dfrac{4T}{4}\) |
| (c) | the velocity is maximum at \(t=\dfrac{T}{4}\) |
| (d) | the potential energy is equal to the kinetic energy of oscillation at \(t=\dfrac{T}{2}\) |
| 1. | (a), (b) and (d) only | 2. | (a), (b) and (c) only |
| 3. | (b), (c) and (d) only | 4. | (c) and (d) only |
The following statements are given for a simple harmonic oscillator.
| (a) | Force acting is directly proportional to the displacement from the mean position and opposite to it. |
| (b) | Motion is periodic. |
| (c) | Acceleration of the oscillator is constant. |
| (d) | The velocity is periodic. |
Choose the correct alternatives:
1. (a), (b), (d)
2. (a), (c)
3. (b), (d)
4. (c), (d)
When a mass \(m\) is connected individually to two springs \(S_1\) and \(S_2,\) the oscillation frequencies are \(\nu_1\) and \(\nu_2.\) If the same mass is attached to the two springs as shown in the figure, the oscillation frequency would be:

| 1. | \(v_2+v_2\) | 2. | \(\sqrt{v_1^2+v_2^2}\) |
| 3. | \(\left(\dfrac{1}{v_1}+\dfrac{1}{v_1}\right)^{-1}\) | 4. | \(\sqrt{v_1^2-v_2^2}\) |
A particle executing SHM has a maximum speed of \(30\) cm/s and a maximum acceleration of \(60\) cm/s2. The period of oscillation is:
1. \(\pi \) s
2. \(\dfrac{\pi }{2}\) s
3. \(2\pi\) s
4. \(\dfrac{\pi }{4}\) s
The equation of motion of a particle is \(x =a \text{cos} ( \alpha t )^{2}\). The motion is:
1. periodic but not oscillatory
2. periodic and oscillatory
3. oscillatory but not periodic
4. neither periodic nor oscillatory
The figure shows the circular motion of a particle. The radius of the circle, the period, the sense of revolution, and the initial position are indicated in the figure. The simple harmonic motion of the \({x\text-}\)projection of the radius vector of the rotating particle \(P\) will be:

1. \(x \left( t \right) = B\text{sin} \left(\dfrac{2 πt}{30}\right)\)
2. \(x \left( t \right) = B\text{cos} \left(\dfrac{πt}{15}\right)\)
3. \(x \left( t \right) = B\text{sin} \left(\dfrac{πt}{15} + \dfrac{\pi}{2}\right)\) \(\)
4. \(x \left( t \right) = B\text{cos} \left(\dfrac{πt}{15} + \dfrac{\pi}{2}\right)\)
Four pendulums \(A,B,C,\) and \(D\) are suspended from the same elastic support as shown in the figure. \(A\) and \(C\) are of the same length, while \(B\) is smaller than \(A\) and \(D\) is large than \(A.\) If \(A\) is given a transverse displacement,

| 1. | \(D\) will vibrate with maximum amplitude. |
| 2. | \(C\) will vibrate with maximum amplitude. |
| 3. | \(B\) will vibrate with maximum amplitude. |
| 4. | All four will oscillate with equal amplitude. |






