The period of oscillation of a mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be
(a) T (b)T/
(c) 2T (d)
नगण्य द्रव्यमान के स्प्रिंग से निलंबित एक द्रव्यमान M का दोलन काल T है। यदि इसके साथ एक और द्रव्यमान M को भी निलंबित किया जाता है, तो दोलन काल अब होगा:
(a) T (b) T/
(c) 2T (d)
A body performs S.H.M. . Its kinetic energy K varies with time t as indicated by graph
(a) 
(c) 
एक निकाय सरल आवर्त गति करता है। इसकी गतिज ऊर्जा K, समय t के साथ परिवर्तित होती है जैसा कि ग्राफ द्वारा दर्शाया गया है
(a) 
(c) 
The period of a simple pendulum measured inside a stationary lift is found to be T. If the lift starts accelerating upwards with acceleration of g/3 then the time period of the pendulum is
(a)
(b)
(c)
(d)
एक स्थिर लिफ्ट के अंदर एक सरल लोलक का दोलन काल T मापा जाता है। यदि लिफ्ट g/3 त्वरण से ऊपर की ओर त्वरित होना प्रारम्भ करती है तब लोलक का दोलन काल है:
(a)
(b)
(c)
(d)
In a simple pendulum, the period of oscillation T is related to length of the pendulum l as
(a) =constant
(b) =constant
(c) =constant
(d) =constant
एक साधारण लोलक में, लोलक का दोलन काल T लोलक की लंबाई l से निम्न रूप से संबंधित है:
(a) = नियतांक
(b) = नियतांक
(c) = नियतांक
(d) = नियतांक
A body is executing Simple Harmonic Motion. At a displacement x its potential energy is and at a displacement y its potential energy is . The potential energy E at displacement is
(a) (b)
(c) (d) None of these.
एक पिंड सरल आवर्त गति कर रहा है। x विस्थापन पर इसकी स्थितिज ऊर्जा है और y विस्थापन पर इसकी स्थितिज ऊर्जा है। विस्थापन पर स्थितिज ऊर्जा E है:
(a) (b)
(c) (d) इनमें से कोई नहीं
The potential energy of a simple harmonic oscillator when the particle is half way to its end point is (where E is the total energy)
(a) (b)
(c) (d)
जब कण अपने अंतिम बिंदु की आधी दूरी पर होता है, एक सरल आवर्ती दोलक की स्थितिज ऊर्जा है (जहाँ E कुल ऊर्जा है)
(a) (b)
(c) (d)
which of the following figure represents damped harmonic motion
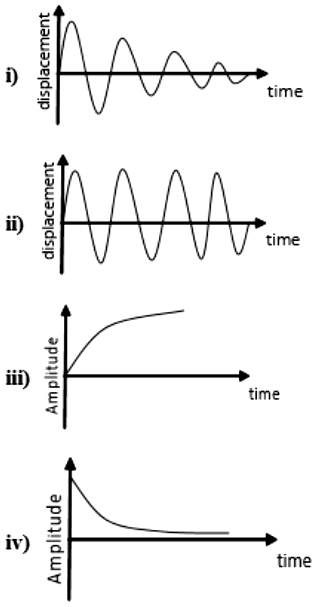
1. i and ii
2. iii and iv
3. i, ii, iii, and iv
4. i, and iv
निम्नलिखित में से कौन सी आकृति अवमंदित आवर्ती गति का निरूपण करती है:
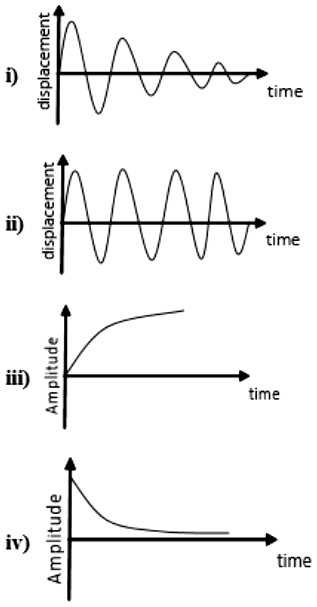
1. i और ii
2. iii और iv
3. i, ii, iii, और iv
4. i, और iv
Two simple harmonic motions of angular frequency 100 and 1000 rad have the same displacement amplitude. The ratio of their maximum acceleration is -
(a) 1:10 (b) 1:
(c) 1: (d) 1:
100 और 1000 rad कोणीय आवृत्ति की दो सरल आवर्त गति के विस्थापन आयाम समान हैं। उनके अधिकतम त्वरण का अनुपात है -
(a) 1:10 (b) 1:
(c) 1: (d) 1:
The angular velocities of three bodies in simple harmonic motion are with their respective amplitudes as . If all the three bodies have same mass and maximum velocity, then
(a) (b)
(b) (d)
सरल आवर्त गति में तीन निकायों के कोणीय वेग हैं उनके आयाम क्रमशः के रूप में हैं। यदि तीनों पिंडों के द्रव्यमान और अधिकतम वेग समान हो, तब
(a) (b)
(c) (d)
The maximum velocity of a simple harmonic motion represented by is given by
(a) 300 (b)
(c) 100 (d)
द्वारा निरूपित एक सरल आवर्त गति का अधिकतम वेग किसके द्वारा दिया गया है?
(a) 300 (b)
(c) 100 (d)









