A particle is projected with a velocity u making an angle $\mathrm{\theta }$ with the horizontal. At any instant, its velocity v is at right angles to its initial velocity u; then v is:

1.  ucos$\mathrm{\theta }$

2.  utan$\mathrm{\theta }$

3.  ucot$\mathrm{\theta }$

4.  usec$\mathrm{\theta }$

A projectile is given an initial velocity of $\hat{i}+2\hat{j}$. The cartesian equation of its path is (g = 10 ${\mathrm{ms}}^{-2}$) 

1. $\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$

2. $\mathrm{y}=\mathrm{x}-5{\mathrm{x}}^2$

3. $4\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$

4. $\mathrm{y}=2\mathrm{x}-25{\mathrm{x}}^2$

A ship A is moving westwards with a speed of 10 km ${\mathrm{h}}^{-1}$ and a ship B, 100 km south of A is moving northwards with a speed of 10 km ${\mathrm{h}}^{-1}$. The time after which the distance between them becomes the shortest, is:

1. 5 hr

2. $5\sqrt{2}$ hr

3. $10\sqrt{2}$ hr

4. 0 hr

Time taken by the projectile to reach from A to B is t. Then the distance AB is equal to :

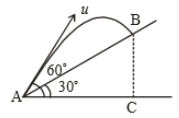
1. $\frac{ut}{\sqrt{3}}$

2. $\frac{\sqrt{3}ut}{2}$

3. $\sqrt{3}ut$

4. 2ut

A particle projected with kinetic energy ${\mathrm{k}}_0$ with an angle of projection $\mathrm{\theta }$. Then the variation of kinetic K with vertical displacement y is

1.  linear

2.  parabolic

3.  hyperbolic

4.  periodic

A river is flowing with a speed of 1 km/hr. A swimmer wants to go to point 'C' starting from 'A'. He swims with a speed of 5 km/hr, at an angle $\theta$ with respect to the river. If \(\text {AB = BC = 400 m}\). Then

1. The time taken by the man is 12 min

2. The time taken by the man is 8 min

3. The value of $\theta$ is 45$°$

4. The value of $\theta$ is 53$°$

 A body is thrown horizontally with a velocity \(\sqrt{2 g h}\) from the top of a tower of height \(h\). It strikes the level ground through the foot of the tower at a distance \(x\) from the tower. The value of \(x\) is:

Two men \(P\) and \(Q\) are standing at corners \(A\) and \(B\) of a square \(ABCD\) of side \(8~\text m.\) They start moving along the track with a constant speed \(2~\text{m/s}\) and \(10~\text {m/s}\) respectively. The time when they will meet for the first time is equal to:
       
1. \(2~\text{sec}\)
2. \(3~\text{sec}\)
3. \(1~\text{sec}\)
4. \(6~\text{sec}\) 

A particle starts from the origin at t=0 and moves in the x-y plane with constant acceleration 'a' in the y direction. Its equation of motion is $y=b{x}^2$. The x component of its velocity (at t=0) is:

(1) variable

(2) $\sqrt{\frac{2a}{b}}$

(3) $\frac{a}{2b}$

(4) $\sqrt{\frac{a}{2b}}$

A body is projected with a velocity \(u\) with an angle of projection \(\theta.\) The change in velocity after the time \((t)\) from the time of projection will be: