Absolute refractive indices of glass and water are 3/2 and 4/3. The ratio of velocity of light in glass and water will be
1. 4:3
2. 8:7
3. 8:9
4. 3:4
Two identical equiconvex thin lenses each of focal lengths \(20\) cm, made of material of refractive index \(1.5\) are placed coaxially in contact as shown. Now, the space between them is filled with a liquid with a refractive index of \(1.5\). The equivalent power of this arrangement will be:

| 1. | \(+5\) D | 2. | zero |
| 3. | \(+2.5\) D | 4. | \(+0.5\) D |
| 1. | \(10\) cm and \(80\) cm |
| 2. | \(85\) cm and \(5\) cm |
| 3. | \(70\) cm and \(20\) cm |
| 4. | \(5\) cm and \(85\) cm |

| 1. | \(\sqrt{2}\) | 2. | \(\sqrt{3}\) |
| 3. | \(\sqrt{3 / 2}\) | 4. | \(\sqrt{4 / 3}\) |
A ray of light incident on an equilateral prism at grazing incidence emerges from the prism at grazing emergence. The Refractive index of the prism is:
| 1. | \(1.5\) | 2. | \(1.8\) |
| 3. | \(1.33\) | 4. | \(2\) |
Which of the following is not due to the total internal reflection of light
1. Brilliance of the diamond
2. Mirage on hot summer days
3. Working of optical fiber
4. Difference between real and apparent depth of a pound
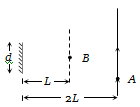
A point source of light B is placed at a distance L in front of the centre of a mirror of width d hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it as shown. The greatest distance over which he can see the image of the light source in the mirror is
1. d/2
2. d
3. 2d
4. 3d
Two plane mirrors, \(A\) and \(B\) are aligned parallel to each other, as shown in the figure. A light ray is incident at an angle of \(30^\circ\) at a point just inside one end of \(A.\) The plane of incidence coincides with the plane of the figure. The maximum number of times the ray undergoes reflections (excluding the first one) before it emerges out is:
1. \(28\)
2. \(30\)
3. \(32\)
4. \(34\)
A concave mirror of focal length \(100\) cm is used to obtain the image of the sun which subtends an angle of \(30'.\) The diameter of the image of the sun will be:
1. \(1.74\) cm
2. \(0.87\) cm
3. \(0.435\) cm
4. \(100\) cm
| 1. | \(4~\text{cm}^2 \) | 2. | \(6~\text{cm}^2 \) |
| 3. | \(16~\text{cm}^2 \) | 4. | \(36~\text{cm}^2 \) |