Two racing cars of masses \(m_1\) and \(m_2\) are moving in circles of radii \(r_1\) and \(r_2\) respectively. Their speeds are such that each makes a complete circle in the same duration of time \(t\). The ratio of the angular speed of the first to the second car is:

1.	\(m_1:m_2\)	2.	\(r_1:r_2\)
3.	\(1:1\)	4.	\(m_1r_1:m_2r_2\)

A particle P is moving in a circle of radius ‘a’ with a uniform speed v. C is the centre of the circle and AB is a diameter. When passing through B the angular velocity of P about A and C are in the ratio 

1. 1 : 1

2. 1 : 2

3. 2 : 1

4. 4 : 1

Two bodies of mass 10 kg and 5 kg moving in concentric orbits of radii R and r such that their periods are the same. Then the ratio between their centripetal acceleration is 

1. R/r

2. r/R

3. R²/r²

4. r²/R²

An electric fan has blades of length 30 cm as measured from the axis of rotation. If the fan is rotating at 1200 r.p.m, the acceleration of a point on the tip of the blade is about

1. 1600 m/sec²

2. 4740 m/sec²

3. 2370 m/sec²

4. 5055 m/sec²

A particle moves with constant speed \(v\) along a circular path of radius \(r\) and completes the circle in time \(T\). The acceleration of the particle is:
1. \(2\pi v / T\)
2. \(2\pi r / T\)
3. \(2\pi r^2 / T\)
4. \(2\pi v^2 / T\)

If a_r and a_t represent radial and tangential accelerations, the motion of a particle will be uniformly circular if:
1. a_r = 0 and a_t = 0
2. a_r = 0 but a_t \(\neq\) 0
3. a_r \(\neq\) 0 but a_t = 0
4. a_r \(\neq\) 0 and a_t \(\neq\) 0$\mathrm{}$
 

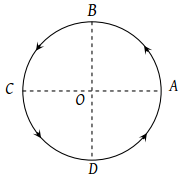
The figure shows a body of mass m moving with a uniform speed v along a circle of radius r. The change in velocity in going from A to B is:

1. $v\sqrt{2}$

2. $v/\sqrt{2}$

3. v

4. zero

An aeroplane is flying horizontally with a velocity u = 600 km/h at a height of 1960 m. When it is vertically at a point A on the ground, a bomb is released from it. The bomb strikes the ground at point B. The distance AB is:

1. 1200 m

2. 0.33 km

3. 3.33 km

4. 33 km

A particle (A) is dropped from a height and another particle (B) is thrown in the horizontal direction with a speed of 5 m/sec from the same height. The correct statement is:

(1) Both particles will reach at ground simultaneously

(2) Both particles will reach at ground with same speed

(3) Particle (A) will reach at ground first with respect to particle (B)

(4) Particle (B) will reach at ground first with respect to particle (A)

An object is thrown along a direction inclined at an angle of 45° with the horizontal direction. The horizontal range of the particle is equal to 

(1) Vertical height

(2) Twice the vertical height

(3) Thrice the vertical height

(4) Four times the vertical height